Пусть  - канонический базис в
- канонический базис в 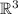 .
.
Тогда матрицу перехода 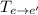 можно найти следующим образом:
можно найти следующим образом:
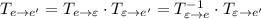
Если записать блочную матрицу 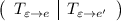 и привести путем элементарных преобразований к виду
и привести путем элементарных преобразований к виду  , то
, то 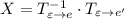
Матрицу 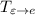 легко получить: достаточно записать в столбцы координаты векторов базиса
легко получить: достаточно записать в столбцы координаты векторов базиса  . Аналогично с матрицей
. Аналогично с матрицей 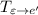 .
.
В итоге необходимо получить вид  следующей матрицы:
следующей матрицы:
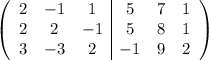
Вычтем первую строку из второй и третьей:
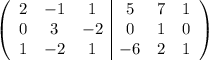
Вычтем из первой строки 2 третьих и поменяем их местами:
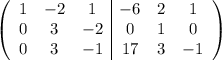
Вычтем из третьей строки вторую:
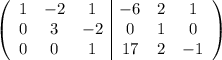
Прибавим ко второй строке 2 третьих и вычтем из первой третью:

Делим вторую строку на 3:
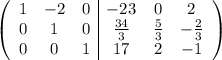
Прибавляем в первой строке 2 вторых:
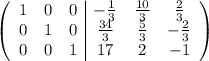
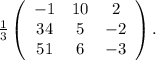
104.
a) cos 120 =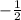
б) sin(-150)= -sin 150=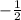
в) tg(-225)= -tg 225 = -1
г) cos(-225)=cos 225=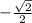
д) cos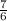
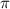 = cos 630 = 0
= cos 630 = 0
е)sin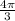 = sin 240 =
= sin 240 =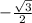
106.
а) sin ( -
-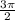 ) = sin (
) = sin ( -270) = sin (270-
-270) = sin (270- ) = -cos
) = -cos 
б) cos ( -
-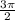 )= cos (
)= cos ( -270) = cos (270-
-270) = cos (270- ) = -sin
) = -sin 
в) tg ( -2
-2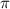 ) = tg (
) = tg ( -360) = tg (360-
-360) = tg (360- ) = -tg
) = -tg 
Объяснение:
104.
cos(-α)= cos α
sin(-α)= -sin α
tg(-α)= -tg α
ctg(-α)= -ctg α
a) cos 120 =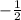
б) sin(-150)= -sin 150=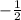 ( т.к. sin непарная функция => sin(-α)= -sin α )
( т.к. sin непарная функция => sin(-α)= -sin α )
в) tg(-225)= -tg 225 = -1 ( т.к. tg непарная функция => tg(-α)= -tg α )
г) cos(-225)=cos 225=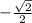 ( т.к. cos парная функция => cos(-α)= cos α )
( т.к. cos парная функция => cos(-α)= cos α )
д) cos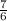
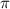 =
=  =630, 630=360+270 ( 360 это один полный оборот)
=630, 630=360+270 ( 360 это один полный оборот)
=> cos 270 cos 270 = 0
е)sin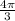 = sin 240 =
= sin 240 =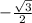
106.
В этом номере я использовал формулы приведения
их можно найти в интернете
а) sin ( -
-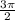 ) = sin (
) = sin ( -270) = sin (270-
-270) = sin (270- ) = -cos
) = -cos 
б) cos ( -
-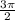 )= cos (
)= cos ( -270) = cos (270-
-270) = cos (270- ) = -sin
) = -sin 
в) tg ( -2
-2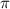 ) = tg (
) = tg ( -360) = tg (360-
-360) = tg (360- ) = -tg
) = -tg 