с)
Функция у = - х - линейная. Так как к = - 1, - 1 < 0, то функция является убывающей на всей области определения.
Своего наибольшего значения на [-π;3] она будет достигать при наименьшем значении аргумента , т.е. при х = - π.
у = π - наибольшее значение функции.
Своего наименьшего значения на [-π;3] она будет достигать при наибольшем значении аргумента , т.е. при х = 3.
у = - 3 - наименьшее значение функции.
d) y = x/2 - 4 - линейная. Так как к = 1/2, 1/2 > 0, то функция является возрастающей на всей области определения.
При х = 4 функция будет достигать наибольшего значения:
у = 4/2 - 4 = -2;
у = - 2 - наибольшее значение функции.
При х = 0 функция будет достигать наименьшего значения:
у = 0/2 - 4 = -4;
у = - 4 - наименьшее значение функции.
ответ: a∈( 0; 1/4)
Объяснение:
ax^2+x-3 = 0
Обязательное условие: уравнение имеет 2 корня
D=1+12a>0 → a > -1/12
a = 0 нам так же не подходит, ибо данное уравнение становится линейным.
Таким образом: a∈(-1/12;0) ∪ ( 0; ∞)
По условию ясно, что число 2 лежит между корнями параболы.
Из графических представлений ясно, что при a>0 между корнями лежит отрицательная часть параболы f(x) = ax^2+x-3, а при a<0 между корнями лежит положительная часть параболы. Данное условие эквивалентно следующему неравенству:
a*f(2)< 0
a(4a-1) < 0
a∈(0; 1/4)
Пересекая с условием: a∈(-1/12;0) ∪ ( 0; ∞), получаем ответ:
a∈(0; 1/4)
По формуле бинома Ньютона
Найдем второй и четвертый член разложения при k = 1 и k = 3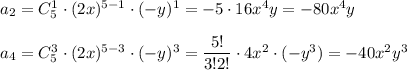
2)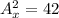
По теореме Виета
ответ: 7.