x1 = cos(π/9)
x2 = cos(5π/9)
x3 = cos(7π/9)
Объяснение:
Предположим, что x > 1
Тогда
x^3 > x
x^3 - x > 0
6x^3 -6x > 0
Таким образом:
8x^3 -6x - 1 = 2x^3 + 6x^3 - 6x - 1 >= 2x^3 - 1 > 0
Если же x < - 1, то x^3<-1
6x^3 - 6x < 0
8x^3 -6x - 1 = 2x^3 + 6x^3 - 6x - 1 <= 2x^3 - 1 < 0
Как видим, если действительное решение существует, то оно принадлежит интервалу:
1<=x<=-1
То есть можно сделать замену:
x = cost
При этом достаточно рассмотреть интервал:
0<=t <= π
8х^3 – 6х – 1 =0
2(4x^3 - 3x) - 1 = 0
2*(4cos^3(t) - 3cos(t) ) - 1 = 0
Заметим, что:
4cos^3(t) - 3cos(t) = cos(3t)
Откуда получаем:
2cos(3t) - 1 = 0
cos(3t) = 1/2
3t = +-π/3 +2πn
t = +-π/9 +2πn/3, где n∈Z
0<=+-π/9 +2πn/3<= π
0 <=6n +- 1 <= 9
Подойдет n = 0 и n = 1
При n = 0 подойдет решение:
t1 = π/9
Откуда:
x1 = cos(t1) = cos(π/9) ≈ 0,94
При n = 1 имеем еще два решения:
t2 = - π/9 + 2π/3 = 6π/9 - π/9 = 5π/9
x2 = cos(5π/9) ≈ - 0.17
t3 = π/9 + 2π/3 = 6π/9 + π/9 = 7π/9
x3 = cos(7π/9) ≈ - 0,77
Объяснение:
Впервую очередь найдем стационарные точки. Для нахождения мы берем производную от исходной функции и приравниваем к нулю
f(x)=12sinx-6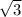
x+
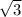π+6
f'(x)=12cosx-6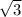
f'(x)=0
12cosx-6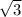
=0
cosx=
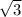/2
x=±π/6+2πk, k∈Z
итак подставляем в место k целые числа начиная с нуля для попадения в промежуток [0; π/2]
k=0;
x₁=π/6
x₂=-π/6 этот корень мы не берем так как не попадает в наш промежуток
k=1
x=π/6+2π=13π/6 уже не попадает в промежуток
значить мы нашли единственную стацианарную точку х теперь подставляем в наш начальную функцию и находим наибольшее значение.
х=π/6; fmax(π/6)=12*sin(π/6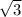)-6
*π/6+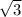
π+6=12