y′′ − 4y′ + 4 = 0
Решим характеристическое уравнение
к²-4к=0;
к*(к-4)=0
к₁=0; к₁=4;
общее решение соответствующего однородного уравнения имеет вид
уобщ. =с₁*е^(0*x)+c₂e^(4х), или уобщ.=с₁+c₂e^(4х)
т.к. y′′ − 4y′=- 4 , то частное решение ищем по правой части, которая представляет из себя многочлен нулевой степени, учитав, что 0-однократный корень характеристического уравнения. значит.
уч.=Ах,
у'=А,
у''=0
для определения А , подставим уч.=Ах, у'=А, у''=0 в исходное уравнение,
-4А=-4, значит, А=1, уч.=х,
зная, что общее решение неоднородного уравнения равно сумме общего решения однородного и частного решения неоднородного,
получим Y=уо.o+yо.н., подставим найденные уо.o и yо.н в это равенство, получим Y=с₁+c₂e^(4х)+х- общее решение неоднородного дифференциального уравнения
найдем первую производную
Y'=(с₁+c₂e^(4х)+х)'=4c₂e^(4х)+1
для нахождения с ₁ и с₂ в задаче Коши подставим начальные условия.
Получим
с₁+c₂e^(4*0)+0=1⇒с₁+c₂=1
4c₂e^(4*0)+1=3⇒c₂=2/4=0.5
зная c₂, найдем с₁=1-c₂=1-0.5=0.5
Значит, частное решение, удовлетворяющее начальным условиям, будет Y=0.5+0.5e^(4х)+х
Во-первых, отметим, что аргументы логарифмов должны быть строго больше нуля, но поскольку аргументы -- целые числа, то они должны быть хотя бы
. С другой стороны, как нетрудно заметить, их сумма равна 
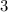. Стало быть, каждый из них равен единице: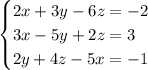 
Детерминант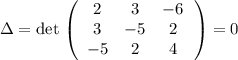
(-(1 строка) - (2 строка) = (3 строка)). Решение можно параметризовать: 
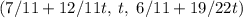, откуда 
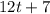должно делиться на 
, а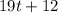 
должно делиться на 
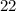. Тогда 
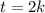, потому 
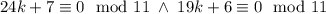. Из первого 
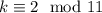, а из второго -- 
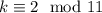. Итак, 
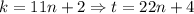, поэтому решение переписывается в виде 
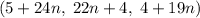. Итак, слева у исходного неравенства стоит нуль, а справа -- 
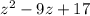. Получаем, что 
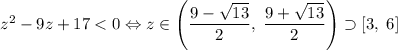, а потому подходит только 
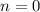и соответствующая тройка 
.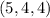