9класс
«квадратичная функция и её график»
вариант 11
постройте график функции y = -x +6x - 5.
найдите с графика:
1.1 значение при х = -0,5;
1.2 значения х, при которых у = 4;
1.3 нули функции;
1.4 промежутки, в которых у > 0, у< 0;
1.2 промежуток, на котором функция возрастает.
• 2. найдите наименьшее значение
функции у = х² - 7х +6
•3. найдите область значений функции
у = х² - 4х +3, где х є [-4; 7].
4. не выполняя построения, определите,
пересекаются ли парабола у =x²-4х +2 и прямая у= 3х -4. если точки пересечения существуют,то найдите их координаты.
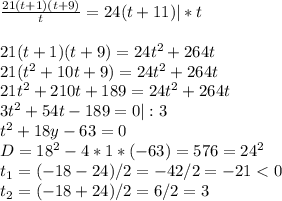
 (км/ч)
(км/ч)
(
a
+
b
)
n
=
∑
k
=
0
n
(
n
k
)
a
n
−
k
b
k
=
(
n
0
)
a
n
+
(
n
1
)
a
n
−
1
b
+
⋯
+
(
n
k
)
a
n
−
k
b
k
+
⋯
+
(
n
n
)
b
n
(a+b)^n = \sum_{k=0}^n \binom{n}{k} a^{n - k} b^k = {n\choose 0}a^n + {n\choose 1}a^{n - 1}b + \dots + {n\choose k}a^{n - k}b^k + \dots + {n\choose n}b^n
где
(
n
k
)
=
n
!
k
!
(
n
−
k
)
!
=
C
n
k
{n\choose k}=\frac{n!}{k!(n - k)!}= C_n^k — биномиальные коэффициенты,
n
n — неотрицательное целое число.
В таком виде эта формула была известна ещё индийским и персидским математикам; Ньютон вывел формулу бинома Ньютона для более общего случая, когда показатель степени — произвольное действительное (или даже комплексное) число.