Пусть b1,b2,b3 члены геометрической прогрессии и a1,a4,a25 соответственно арифметической, из условия следует что b1+b2+b3=114. Из свойств арифм прогрессии, приравнивая соответствующие члены перепишем их как b1=a1, b2=a1+3d, b3=a1+24d суммируя получаем b1+b2+b3=3a1+27d=114 откуда a1+9d=38, выразим отсюда a1=38-9d так как b2/b1=b3/b2 или что тоже самое (a1+3d)/a1=(a1+24d)/(a1+3d) подставляя в уравнение, выражение a1=38-9d получаем (38-6d)/(38-9d)=(38+15d)/(38-6d) или (38-6d)(38-6d)=(38+15d)(38-9d) 18*38*d=171d^2 откуда d=0,d=4 при d=0 ответ b1=b2=b3=38 , при d=4, a1=2 получаем b1=a1=2, b2=a4=14, b3=a25=98.
сверху первый. В примере а) 2 корня. (я расписала подробно, но ты можешь решить так как я решила пример в б)
Б) D= 1^2-4*2*5
D=-39
корней нет.
2. а) D=(-11)^2-4*1*(-42) = 289 =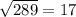
б) решу методом замены переменной:
y^2-13y+36=0
D=(-13)^2-4*36=25=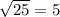
x^2=9 x^2=4
в) D=5^2-4*2*2 = 25-16 = 9 =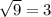
3. Длина первого катета - х см, тогда длина второго катета
будет (х + 5) см.
Площадь прямоугольного треугольника вычисляется по формуле:
S =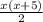
x*(x + 5) = 42*2
x² + 5x - 84 = 0
D = 25 + 4*1*84 = 361 =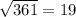
x₁ = (- 5 - 19)/2
x₁ = - 24/2 = - 12 посторонний корень
x₂ = (- 5 + 19)/2
x₂ = 7
7 см - длина первого катета
1) 7 + 5 = 12 (см) - длина второго катета
ответ: 7 см, 12 см