мой ответ такой
..................
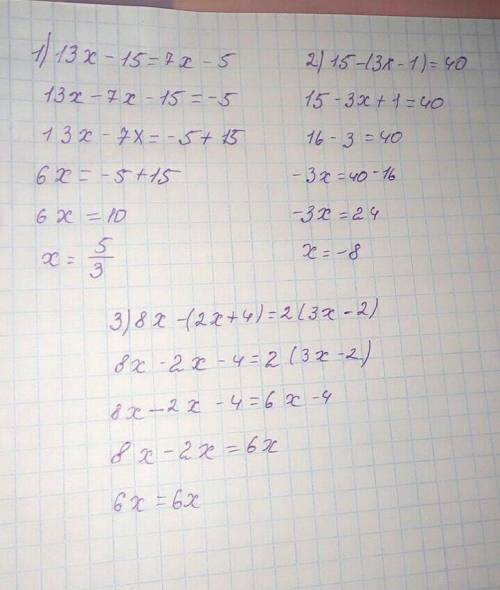
будет -1
Выражение: 1+(-4)^2*(-1//2)^3
ответ: -1
Решаем по действиям:
1) (-4)^2=16
(-4)^2=(-1)^2*4^2
1.1) (-1)^2=1
X-1
_-_1_
1
1.2) 4^2=16
X4
_4_
16
2) 1//2=0.5
1.0|2_ _
1_0_|0.5
0
3) (-0.5)^3=(-1)*0.125
(-0.5)^3=(-1)^3*0.5^3
3.1) (-1)^3=(-1)
X-1 X-1
_-_1_ _ _1_
1 -1
3.2) 0.5^3=0.125
X0.5 X0.25
_0_._5_ _ _ _0_._5_ _
25 125
0_0_ _ _ 0_0_0_ _ _
0.25 0.125
4) 16*(-1)=-16
5) (-16)*0.125=-16*0.125
6) 16*0.125=2
X0.125
_ _ _1_6_
0750
0_1_2_5_ _
2
7) 1+(-2)=1-2
8) 1-2=-1
-2
_1_
-1
Решаем по шагам:
1) 1+16*(-(1//2))^3
1.1) (-4)^2=16
(-4)^2=(-1)^2*4^2
1.1.1) (-1)^2=1
X-1
_-_1_
1
1.1.2) 4^2=16
X4
_4_
16
2) 1+16*(-0.5)^3
2.1) 1//2=0.5
1.0|2_ _
1_0_|0.5
0
3) 1+16*(-1)*0.125
3.1) (-0.5)^3=(-1)*0.125
(-0.5)^3=(-1)^3*0.5^3
3.1.1) (-1)^3=(-1)
X-1 X-1
_-_1_ _ _1_
1 -1
3.1.2) 0.5^3=0.125
X0.5 X0.25
_0_._5_ _ _ _0_._5_ _
25 125
0_0_ _ _ 0_0_0_ _ _
0.25 0.125
4) 1+(-16)*0.125
4.1) 16*(-1)=-16
5) 1+(-16*0.125)
5.1) (-16)*0.125=-16*0.125
6) 1+(-2)
6.1) 16*0.125=2
X0.125
_ _ _1_6_
0750
0_1_2_5_ _
2
7) 1-2
7.1) 1+(-2)=1-2
8) -1
8.1) 1-2=-1
-2
_1_
-1
Есть очень известная теорема Ферма-Эйлера, вот её формулировка:
Нечётное простое число представимо в виде суммы квадратов двух натуральных чисел тогда и только тогда, когда оно имеет вид
4k + 1 где k - нат. число.
Пусть наши числа х и y. Тогда по этой теореме
х = 4m + 1 , y = 4n + 1 (где n, m - нат. числа)
Рассмотрим произведение чисел х и y
хy = (4m + 1)(4n + 1) = 16mn + 4m + 4n + 1 = 4*(4mn + m + n) + 1 =>
обозначив выражение 4mn + m + n чрез некое натуральное число q имеем
хy = 4q + 1
тогда по этой же теореме произведение хy представимо в виде суммы квадратов двух натуральных чисел..
Объяснение:
1)13х-15= 7х-5
13х-7х =-5+15
6х=10
х=10/6=5/3
2)15 - (3x-1)=40
3х-1=15-40
3х-1=-25
3х=1-25
3х=-24
х=-8
3)8x - (2x + 4) = 2 * (3x - 2);
8х - 2х - 4 = 6х - 4;
8х - 2х - 6х = -4 + 4;
0 = 0;