Question

Найти производную, подробное решение: (2x-3)^5(3x^2+2x+1)

Answer 1

$10(2x-3)^4\cdot (3x^2+2x+1) + (2x-3)^5\cdot (6x+2)$

Объяснение:

Для начала необходимо понять, что данное выражение представляет собой произведение двух функций, а для производной от произведения функций существует правило:

$(f(x)g(x))' = f'(x)g(x) + f(x)g'(x)$

В данном случае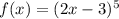 $f(x)=(2x-3)^5$, а $g(x)=3x^2+2x+1$

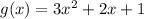
Итак, нам потребуется производная от функции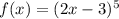 $f(x)=(2x-3)^5$, которая является сложной функцией, производная от которой берется по следующему правилу:

$(u(v(x)))' = u'(v(x))v'(x)$

Здесь $u(v(x))=(2x-3)^5$, $v(x)=2x-3$

$u(v(x))$ - степенная функция, для нее правило такое:

$(x^n)' = nx^{n-1}$

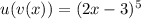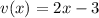
Вычисляем:

$f'(x)=(u(v(x)))'=((2x-3)^5)' = 5(2x-3)^4\cdot 2 = 10(2x-3)^4$

$5(2x-3)^4$ мы получили, когда брали производную от внешней степенной функции , двойка появилась в результате взятия производной от $v(x)=2x-3$. Т.е. $(2x-3)'=2$

---

Теперь возьмем производную от второго сомножителя в исходном выражении:

$g'(x)=(3x^2+2x+1)' = 3\cdot2x+2 = 6x+2$

Подставляем все в формулу: $\[(f(x)g(x))' = f'(x)g(x) + f(x)g'(x)\]$

$10(2x-3)^4\cdot (3x^2+2x+1) + (2x-3)^5\cdot (6x+2)$