1) Переносим x из правой части уравнения в левую, изменив знак 2x < x + 7 x < 7 Например, можно подставить вместо х 5 или 3, они будут меньше 7. 2) 3x > 15 Делим обе части неравенства на 3 x > 5 3) -4 < -16 Скорее всего вы здесь пропустили х:) Скорее всего оно было рядом с -4 -4x < -16 Делим обе части неравенства на (-4) Заметь, что если мы делим на отрицательное число, то знак меняется на противоположный x > 4 3) 5x + 1 > 11 Переносим 1 в другую часть 5x > 10 Делим обе части неравенства на 5 x > 2 Например, решениями могут быть 3, 5, 10, т.к. они все больше двух
Пусть знаменатель дроби х, числитель (х-7). Дробь (х-7)/х. Если числитель этой дроби уменьшить на 1 , а знаменатель увеличить на 4, то получим дробь ((х-7)-1)/(х+4)=(х-8)/(х+4). По условию дробь уменьшится на 1/6. Уравнение (х-7)/х - (1/6)=(х-8)/(х+4).
Умножаем на 6х(х+4)≠0. 6(х+4)(х-7)-х(х+4)=6х(х-8); х²-26х+168=0 D=(-26)²-4·168=676-672=4. x=(26-2)/2=12 или х=(26+2)/2=14
х-7=12-7=5 или х-7=14-7=7 дробь 5/12 7/14 (5-1)/(12+4)=4/16=1/4- (7-1)/(14+4)=6/18=1/3 новая дробь (5/12)-(1/6)=(5/12)-(2/12)=3/12=1/4 (7/14)-(1/6)=(21/42)- (7/42)=14/42= =1/3
3-3x-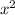 =-7
=-7
x=-5
x=2
y=18
y=-3
(x1, y1)=(-5, 18)
(x2, y2)=(2, -3)
(x1, y1)=(-5, 18)
(x2, y2)=(2, -3)
Объяснение: