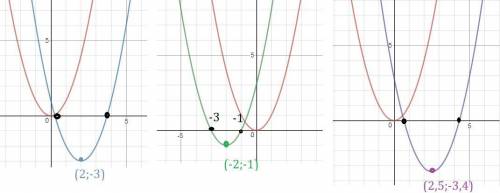
1) Шаблон y=x²
Вершина в точке (2;-3)
Нули функции
(x-2)²-3=0 ⇒
(x-2)²=3
x-2= -√3 или х-2=√3
х=2-√3 или х=2+√3
2) Шаблон y=x²
Вершина в точке (-2;-1)
Нули функции
(x+2)²-1=0 ⇒
(x+2)²=1
x+2= -1 или х+2=1
х=-3 или х=-1
3) Шаблон y=x²
Вершина в точке (2,5;-3,4)
Нули функции
(x-2,5)²-3,4=0 ⇒
(x-2,5)²=3,4
x-2,5= -√3,4 или x-2,5=√3,4
х= 2,5 -√3,4 или х=2,5 +√3,4
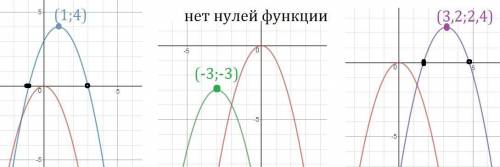
4)Шаблон y= - x²
Вершина в точке (1;4)
Нули функции
-(x-1)²+4=0 ⇒
(x-1)²=4
x-1= -2 или x-1=2
х= -1 или х=3
5)Шаблон y= - x²
Вершина в точке (-3;-3)
Нули функции
-(x+3)²-3=0 ⇒
(x+3)²=-3
уравнение не имеет корней.
Парабола не пересекает ось Ох
6)Шаблон y= - x²
Вершина в точке (3,2;2,4)
Нули функции
-(x-3,2)²+2,4=0 ⇒
(x-3,2)²=2,4
x-3,2= - √2,4 или x-3,2= √2,4
x= 3,2 - √2,4 или x = 3,2+ √2,4
Пусть скорость мотоциклиста после остановки x км/ч, тогда до остановки он двигался со скоростью (x−15) км/ч.
За счёт увеличения скорости на расстоянии 60 км он ликвидировал отставание 12 мин = ⅕ часа. составляем уравнение:
60/(x−15) − 60/x = ⅕;
300(x−(x−15))/[x(x−15)] = 1;
x²−15x−4500 = 0;
x = (15+√(225+18 000))/2 = (15+135)/2 = 75 (км/ч).
Проверяем: до остановки мотоциклист ехал со скоростью 75−15 = 60 км/ч;
тогда 60/60 − 60/75 = 1−⅘ = ⅕ (Ok).
ОТВЕТ: после остановки мотоциклист ехал со скоростью 75 км/ч.
Объяснение:
Для начала разделим 40 на 8 и получим 5. x^2 сокращается частично, x в знаменателе cокращается полностью(встречи с ним ты уже не жди).
Получаем: 5xy - 6xy = -xy
Пример 2.
s^2 сокращается частично, t^2 сокращается частично. В знаменателе s и t полностью сократятся.
4/9 * 3/2 = 2/3st
2/3st + 1/3st = 3/3st = st
Задача решена.