т.к. при выкладывании по 8 и 9 плиток не получается ровного ряда, то количество плиток — такое число, которое делится на 8 и 9 с остатками.
у числа, делящегося на 8 остаток не может быть больше семи. по условию это число на 6 больше, чем при делении на 9. хзначит остаток от деления на 8 может быть равен только 7, а остаток от деления на 9 равен 1.
также количество плиток меньше ста, т.к. тогда бы их хватило на квадратную площадку 10×10.
среди чисее меньше ста надо найти такое, которое делится на 8 с остатком 7 и на 9 с остатком один.
начнём с восьми: остаток 7 означает, что число должно быть на единицу меньше, чем числа, которые делятся на 8 ровно, т.е.: 15, 23, 31, 39, 47, 55, 63, 72.
девять: число с остатком 1 означает, что искомое число на единицу больше, чем допустим числа в таблице умножения на девять, т.е.: 19, 28, 37, 46, 55, 64, 74.
из всех перечисленных чисел видно, что совпадает только одно.
ответ: 55 плиток
1)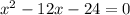
данное уравнение имеет два различных корня.
по теореме Виета:
Т.к. произведение корней отрицательно, то два корня разных знаков: меньший - отрицательный, больший - положительный.
2)
уравнение имеет два различных корня.
по теореме Виета:
Т.к. произведение корней положительно, то имеет два корня одного знака, а т.к. сумма корней положительна, то имеет два положительных корня.
3)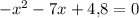
уравнение имеет два различных корня. По т. Виета:
Т.к. произведение корней отрицательно, то имеет два корня различных знаков: меньший - отрицательный, больший - положительный.
4)
уравнение имеет два различных корня. По т. Виета:
Т.к. произведение корней отрицательно, то имеет два корня разных знаков: меньший - отрицательный, больший - положительный.