Заметим, что данное неравенство хорошо раскладывается на множители:
Решим неравенство по методу интервалов.
1)
2)
Введем функции и . Заметим, что первая функция возрастает, а вторая убывает. Поэтому, если уравнение имеет корень, он единственный. Теперь заметим, что x=2 - корень уравнения. Действительно, , верно. Так, мы решили это уравнение, получив, что его корень x=2.
А) В данном прямоугольном треугольнике два угла равны по 45°, значит треугольник равнобедренный; пусть а - катеты, тогда гипотенуза равна а√2 (можно найти по т. Пифагора); синус угла - это отношение противолежащего катета к гипотенузе, поэтому sin 45°=а/(а√2)=1/√2=2/√2. б) π/4=45°, треугольник равнобедренный; пусть а - катеты, тогда гипотенуза равна а√2, косинус угла - это отношение прилежащего катета к гипотенузе, поэтому cos π/4=а/(а√2)=1/√2=√2/2. в) sin π/6=sin 30°. Свойство: в прямоугольном треугольнике катет, который лежит напротив угла 30°, равен половине гипотенузы. Пусть катет, лежащий напротив угла в 30°, равен а, тогда гипотенуза равна 2а. Синус угла - отношение противолежащего угла к гипотенузе, поэтому sin π/6=a/(2a)=1/2. г) cos 30°. Рассуждение аналогично примеру в). Пусть а - катет, противолежащий углу 30°, гипотенуза равна 2а, по т.Пифагора катет, прилежащий углу 30° равен а√3. Косинус угла - отношение прилежащего катета к гипотенузе, поэтому cos 30°=а√3/(2а)=√3/2. д) sin 60°. Второй угол равен 30°. Пусть а - катет, противолежащий углу 30°, гипотенуза равна 2а, второй катет равен а√3. sin 60°=a√3/(2a)=√3/2. е) cos π/3=60°. Второй угол равен 30°. Пусть а - катет, противолежащий углу 30°, гипотенуза равна 2а. cos π/3=a/(2a)=1/2.
Объяснение:
Рассмотрим сначала первое неравенство системы.
Начнем с ОДЗ:
Продолжим решение:
1)
Замена: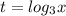 .
.
Обратная замена:
С учетом ОДЗ оба корня подходят.
2)
С учетом ОДЗ получим, что решение неравенства:
Теперь перейдем ко второму неравенству системы:
Понятно, что сначала нужно написать ОДЗ.
Продолжим решение:
Заметим, что данное неравенство хорошо раскладывается на множители:
Решим неравенство по методу интервалов.
1)
2)
Введем функции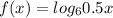 и
и 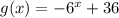 . Заметим, что первая функция возрастает, а вторая убывает. Поэтому, если уравнение имеет корень, он единственный. Теперь заметим, что x=2 - корень уравнения. Действительно,
. Заметим, что первая функция возрастает, а вторая убывает. Поэтому, если уравнение имеет корень, он единственный. Теперь заметим, что x=2 - корень уравнения. Действительно, 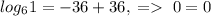 , верно. Так, мы решили это уравнение, получив, что его корень x=2.
, верно. Так, мы решили это уравнение, получив, что его корень x=2.
Тогда решение неравенства с учетом ОДЗ:
Итого имеем:
Найдем пересечение:
Задание выполнено!