для начала находим корни данного в условии уравнения x^2-3x+1=0
D=9-4=13
x1=[3+кореньиз(13)]/2
x2=[3-кореньиз(13)]/2
Составьте уравнение корни которого на 1 больше корней уравнени:
Наши новые корни X=x1+1 и X=x2+1 получаем X=[5+кореньиз(13)]/2
X=[5-кореньиз(13)]/2
Воспользуемся теоремой Виета ,которая говорит нам: x^2+px+q=0
x1+x2=-p
x1*x2=q
Подставим в эту теорему наши новые корни (которые на 1 больше старых ):
[5+кореньиз(13)]/2+[5-кореньиз(13)]/2=-p
[5+кореньиз(13)]/2*[5-кореньиз(13)]/2=q
Таким образом наше квадратное уравнение (которое просят составить в условии) примет вид : x^2-5x+[(25-13)]/2=0-->> конечный вид x^2-5x+6=0
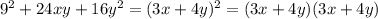
возможно 5 случая:
1) допустим, х-отрицательное, а y положительноетогда сумма (3x+4y) будет отрицательной, а произведение (3x+4y)(3x+4y) будет положительно.(тоже самое будет, если наоборот y-отрицательное, а x положительное)
2) допустим, х и y отрицательные,тогда сумма (3x+4y) будет положительна и произведение (3x+4y)(3x+4y) тоже будет положительно.
3) допустим, х и y положительные, тогда сумма (3x+4y) будет положительна и произведение (3x+4y)(3x+4y) соответственно будет положительно
4) допустим любая из переменных x или y=0, тогда независимо от неравной нулю переменной произведение (3x+4y)(3x+4y) будет положительно
и 5) самый простой случай, когда и х и y =0, тогда и сумма и произведение будут равны нулю, т.е. неотрицательны.
во всех 4х случаях выходит, что выражение неотрицательно, ч.т.д.
Так как квадрат не может быть равен отрицательному числу то уравнение не имеет решений на множестве действительных чисел.
Комплексные корни: