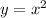 - это парабола, с вершиной в точке (0;0). Она симметрична относительно оси OY. Ветви направлены вверх. Проходит через точки (0;0), (2;4), (-2;4)
- это парабола, с вершиной в точке (0;0). Она симметрична относительно оси OY. Ветви направлены вверх. Проходит через точки (0;0), (2;4), (-2;4)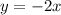 - это прямая, для её построения достаточно 2х точек. Например (0;0) и (-2;4)
- это прямая, для её построения достаточно 2х точек. Например (0;0) и (-2;4)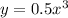 - кубическая парабола. График симметричен относительно начала координат, т.е. точки (0;0).
- кубическая парабола. График симметричен относительно начала координат, т.е. точки (0;0). 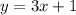 - прямая, проходящая через точки (0;1), (1;4)
- прямая, проходящая через точки (0;1), (1;4)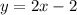 - прямая, проходящая через точки (0;-2) и (1;0)
- прямая, проходящая через точки (0;-2) и (1;0)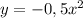 - парабола, с вершиной в точке (0;0), симметричная относительно OY. Ветви направлены вниз.
- парабола, с вершиной в точке (0;0), симметричная относительно OY. Ветви направлены вниз. 
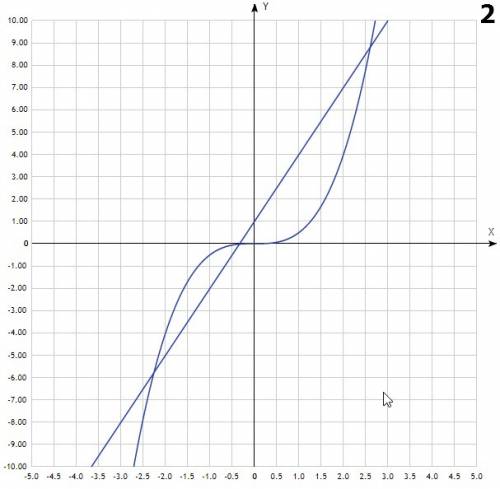
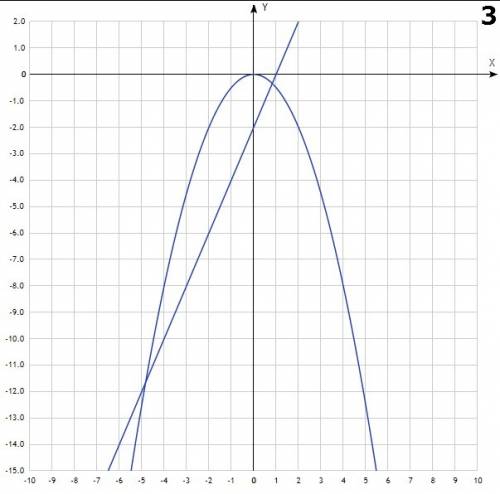
g(x) = x^3 + x
Объяснение:
Пусть имеется произвольная функция f(x). Ее точкой с абсциссой x0 является (x0; f(x0)). По условию, дано правило, по которому точке x0 сопоставляют произведение координат точки для f(x). То есть x0 * f(x0).
Таким образом, получается однозначное соответствие x0 -> x0*f(x0), поэтому его можно назвать функцией g(x) = x*f(x).
По условию, f(x) = x^2 + 1. Тогда искомая функция g(x) = x*(x^2 + 1) = x^3 + x.