Question

Вобщем решить и разжевать мне, что и как у вас получилось, буду . ничего не понимаю про эти линейные уравнения. ​

Answer 1

Нам нужно составить линейную систему уравнений вида

$$\left \{ {{a\cdot x+b\cdot y=e} \atop {c\cdot x+d\cdot y=f}} \right.$

Вместо коэффициентов a,b,c,d подставляем какие-то числа, которые нам в голову придут, чтобы вычислить e и f подставим ещё x,y из задания

a)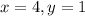 $x=4, y=1$

Пусть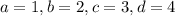 $a=1,b=2,c=3,d=4$

$1\cdot 4 +2\cdot 1=6=e;\\ 3\cdot 4+4\cdot 1 =16=f;$

Получаем систему

$$\left \{ {{x+2y=6} \atop {3x+4y=16}} \right.$

Решим её

$$\left \{ {{x=6-2y} \atop {3(6-2y)+4y=16}} \right.\Rightarrow \left \{ {{x=6-2y} \atop {18-6y+4y=16}} \right. \Rightarrow \left \{ {{x=6-2y} \atop {2y=2}} \right. \Rightarrow \left \{ {{x=4} \atop {y=1}} \right.$

Решение действительно как в задании, значит, все верно сделано.

Аналогично со второй системой

б) пусть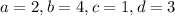 $a=2,b=4, c=1,d=3$

$2\cdot 0+4\cdot 3 = 12=e\\ 1\cdot 0+3\cdot 3 = 9 = f$

Система:

$$\left \{ {{2x+4y=12} \atop {x+3y=9}} \right. \Rightarrow \left \{ {{2(9-3y)+4y=12} \atop {x=9-3y}} \right.\Rightarrow \left \{ {{18-6y+4y=12} \atop {x=9-3y}} \right.$

$$\Rightarrow \left \{ {{2y=6} \atop {x=9-3y}} \right. \Rightarrow \left \{ {{y=3} \atop {x=0}} \right.$

Решение совпадает с тем, что указано в задании, все верно.

P.S. по поводу придумывания коэффициентов.

1. Они не должны быть все нулевые

2. Любое из двух уравнений системы не должно выводиться из другого уравнения системы. Пример:

$$\left \{ {{x+y=5 } \atop {2x+2y=10}} \right.$

Видно, что второе уравнение - первое уравнение, умноженное на 2. Такого тоже не должно быть. Вообще такие уравнения являются линейно зависимыми.

То есть не все числа подойдут, небольшое ограничение есть)