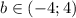Если D < 0, то квадратное уравнение корней не имеет. , т.е.
Это неравенство эквивалентно двойному неравенству
При данное уравнение корней не будет иметь.
Теперь рассмотрим случай когда квадратное уравнение относительно t имеет корни, т.е. , то нам нужны отрицательные корни, поскольку при замене это уравнение не будет иметь корень. По теореме Виета имеем:
Если коэффициенты при х и у совпадают, но свободные члены не равны, то система уравнений не имеет решений, т.е. при а=15 данная система не имеет решений: {6x-15y=-27 {6x-15y=20 => -27≠20 => система не имеет решений при а=15
Если совпадают и коэффициенты при переменных х и у и свободные члены, то система имеет бесконечное множество решений. В данном случае, не существует такого а, при котором бы данная система имела бы беск. мн-во решений.
Мы видим,что уроки по 45 мин.Находим всю продолжительность уроков(всего уроков 5): 45*5=225мин. Уроки были сокращены на 20%,т.е. в тот день они длились 80%.Находим: 225мин.-100% х мин.-80% х=(225*80)/100=180 мин.=3 часа длились уроки в тот день.
Перемены мы видим,что по 15 мин.Находим всю продолжительность перемен(всего их 4): 15*4=60 мин. Перемены были сокращены на 50%,т.е. в 2 раза.Получаем,что в тот день перемены длились 60/2=30 мин. Уроки начались в 8.00. Находим во сколько уроки закончатся в тот день: 8 часов+ 3 часа + 30 минут=11 часов 30 минут, т.е. в 11.30 ответ:в 11.30
Выполним замену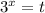 причем
причем 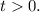 Получаем
Получаем
Дискриминант квадратного уравнения:
Если D < 0, то квадратное уравнение корней не имеет. , т.е.
Это неравенство эквивалентно двойному неравенству
При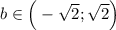 данное уравнение корней не будет иметь.
данное уравнение корней не будет иметь.
Теперь рассмотрим случай когда квадратное уравнение относительно t имеет корни, т.е.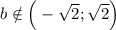 , то нам нужны отрицательные корни, поскольку при замене
, то нам нужны отрицательные корни, поскольку при замене 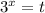 это уравнение не будет иметь корень. По теореме Виета имеем:
это уравнение не будет иметь корень. По теореме Виета имеем:
С учетом существования корней имеем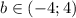
ответ: при