При каких a неравенство (2a-3)cosx -5 >0 не имеет решения.а) { 2a -3 < 0 ;cosx < 5/(2a-3).⇔{ a < 1,5 ;cosx < 5/(2a-3) . не имеет решения , если 5/(2a-3) ≤ -1⇔5/(2a-3)+1 ≤ 0 ⇔(a+1)/(a-1,5) ≤ 0. a∈ [-1 ;1,5) .
б) 2a-3 =0 неравенство не имеет решения. a =1,5.
в) { 2a -3 > 0 ;cosx > 5/(2a-3)..⇔{ a > 1,5 ;cosx > 5/(2a-3) . не имеет решения , если 5/(2a-3) ≥1⇔5/(2a-3)-1 ≥ 0 ⇔(a-4)/(a-1,5) ≤ 0. a∈ (1,5 ; .4].
Такие уравнения решаются по одному приёму: надо снять знак модуля. При этом учитывать, что |x| = x при х ≥ 0 |x| = -x при х <0 Придётся определять какое число стоит под знаком модуля, чтобы потом этот самый знак снять. каждое подмодульное выражение = 0 при х = -2, 3, 2 Поставим эти числа на координатной прямой -∞ -2 2 3 +∞ Получили 4 промежутка. на каждом отдельно будет уравнение иметь свой вид а) (-∞; -2) -(х+2) +(х-3) +(х-2) = 3 -х-2+х-3+х-2 = 3 х = 10 ( в указанный промежуток не входит) б)[-2; 2) х+2 +х -3 +х-2 = 3 3х = 6 х = 2 ( в указанный промежуток не входит) в) [2; 3) х +2 +х -3 -х -2 = 3 х =6 ( в указанный промежуток не входит) г)[3; +∞) х +2 -х+3 -х+2 = 3 -х = -4 х = 4 ( в указанный промежуток входит) ответ: 4
ответ: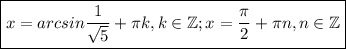
В общем виде суть метода дополнительного аргумента:
Ну и учитываем, что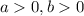 . (знак
. (знак  уже учитывает отрицательные значения
уже учитывает отрицательные значения 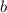 , а если a<0, то выносим (-1) за скобки и работаем по схеме).
, а если a<0, то выносим (-1) за скобки и работаем по схеме).