41-32х≥0;
9-3х≥0
5+х≥0
ОДЗ: х ∈[-5; 41/32]
Перепишем уравнение в виде
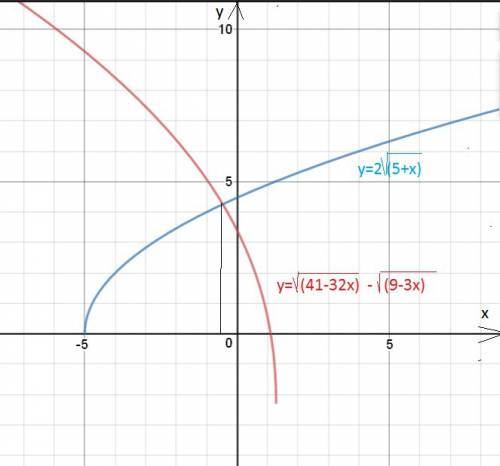
√(41-32x)=2√(5+x)+√(9-3x)
Возводим в квадрат.
41-32х=4(5+х)+4√(5+х)·√(9-3х)+9-3х
4√(5+х)·√(9-3х)=12-33х
Возводим в квадрат при условии 12-33х≥0 ⇒ х ≤12/33.
16(5+х)(9-3х)=144-792х+1089х²;
1137х²-696х-576=0
379х²-232х-192=0
D=(-232)²-4·379·(-192)=53 824+291 072=344 896
x=(232-√344896)/758≈-0,47 или х=(232+√344896)/758≈1,08 - не удовлетворяет условию х ≤12/33, поэтому не является корнем уравнения
50-29,75=20,25 (р)-общая сумма,на которую была снидена цена
предположим,что в первый раз сумма скидки составила х(руб), во второй у(руб),всего х+у=20,25
первый раз снизили товар на z%, во второй на 2z%
x=50*z/100=z/2 руб(сумма скидки в первой раз)
50-z/2руб-стоимость товара после первой уценки
у=(50-z)/2*2z/100=z*(100-z)/100 (сумма скидки во второй раз)
подставим найденные х и у в уравнение z/2+z*(100-z)/100=20,25
после приведения подобных получаем уравнение z²-150z+2025=0
находим корни квадратного уравнения и полуяаем z1=15 ;z2=135
отсюда следует что первый раз товар уценили на 15%, второй на 30%
первый раз на 7,5 руб , второй на 12,75 руб ,в сумме на это даёт 20,25 руб т.е после уценки на 20,25руб товар стал стоит 29,75руб
коофицент=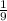
старший=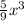
Объяснение: