х³=3-2х
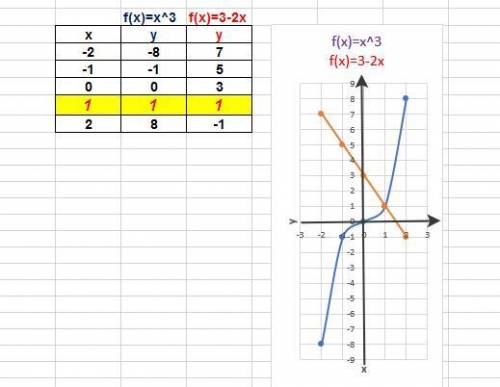
В одной координатной плоскости построить графики левой (кубическая парабола) и правой (прямая) сторон уравнения. Для этого нужно разделить уравнение на две функции f(x)=x³ и f(x)=3-2x.
Значение переменной х в точке пересечения 2-х графиков является корнем данного уравнения.
х=1
График во вложении
Проверка:
x³=3-2x
x³+2x-3=0
2x+x³-1-2=0
(x³-1)+(2x-2)=0
(x-1)(x²+x+1)+2(x-1)=0
↑использована формула разности кубов (a-b)(a²+ab+b²) и вынесение общего множителя за скобки ab-a=a(b-1)
(x-1)(x²+x+3)=0
x-1=0 => x=1, или
x²+x=3=0
D=1²-4*3=1-12=-11 - нет корней, дискриминат - отрицательное число, значит:
x=1
х³=3-2х, при х=1,
1³=3-2*1
1=1
1) sinx=t -1<=t<=1 t^2-3-2t=0 t1=-1 t2=3
t=-1 sinx=-1 x=-П/2+-2пk, k Z
2) 2t^2+t-1=0 t=1/2 t=-1
t=-1 sinx=-1 x=-П/2+-2пk, k Z
t=1/2 sinx=1/2 x=(-1)^k*п/6+Пk
3)tg^3x-tgx=0 tgx*(tg^2x-1)=0
tgx=0 x=Пk
tgx=+-1 x=+-П/4+Пk
4) 2cos^2x=3sinx+2
2*(1-sin^2x)=3sinx+2
2-2sin^2x=3sinx+2
3sinx+2sin^2x=0
sinx=0 x=пk
sinx(3+2sinx)=0