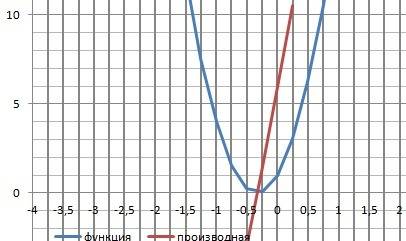
1.Область определения D(x) - Х∈(-∞;+∞) - непрерывная. Вертикальных асимптот - нет
2. Пересечение с осью Х. Решаем квадратное уравнение: Y=0
при х1,2 = - 1/3.
3. Пересечение с осью У. У(0) = 1.
4. Поведение на бесконечности.limY(-∞) = + ∞ limY(+∞) = +∞ - горизонтальных асимптот - нет.
5. Исследование на чётность.Y(-x) = 9*x² - 6*x+1 ≠ Y(x).
Функция ни чётная ни нечётная.
6. Производная функции.Y'(x)= 18*x -6 = 0.
Корень Х= -1/3.
7. Локальные экстремумы. Минимум – Ymin(- 1/3) =0.
8. Интервалы возрастания и убывания. Возрастает - Х∈(-1/3;+∞),
убывает = Х∈(-∞;-1/3)
8. Вторая производная - Y"(x) = 18.
Корня производной - точка перегиба - нет.
9. Вогнутая – «ложка» Х∈(-∞;+∞).
10. Область значений Е(у) У∈(0;+∞)
11. Наклонная асимптота -. Уравнение: lim(oo)(k*x+b – f(x).
k=lim(∞)(9x+6+1)= ∞ - наклонных асимптот - нет
12. График в приложении.
Метод интервалов позволяет решить его за пару минут.В левой части этого неравенства – дробно-рациональная функция. Рациональная, потому что не содержит ни корней, ни синусов, ни логарифмов – только рациональные выражения. В правой – нуль.Метод интервалов основан на следующем свойстве дробно-рациональной функции.Дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует. Найдем нули функции в левой части нашего неравенства. Для этого разложим числитель на множители. Напомним, как раскладывается на множители квадратный трехчлен, то есть выражение вида . Рисуем ось и расставляем точки, в которых числитель и знаменатель обращаются в нуль.Эти точки разбивают ось на N промежутков.Определим знак дробно-рациональной функции в левой части нашего неравенства на каждом из этих промежутков. Мы помним, что дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует. Это значит, что на каждом из промежутков между точками, где числитель или знаменатель обращаются в нуль, знак выражения в левой части неравенства будет постоянным — либо «плюс», либо «минус».