Рассмотрим две функции g(x) = x и f(x) = arcsin x.
g(x) = x - линейная, строго монотонно возрастающая, нечётная непрерывная функция, D(g) = R. График - прямая линия, проходящая через начало координат.
f(x) = arcsin x - обратная тригонометрическая, строго монотонно возрастающая, нечётная непрерывная функция, D(f) = [-1; 1]. График - кривая линия, проходящая через начало координат.
Оба графика проходят через начало координат (0;0).
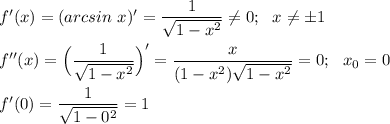
Прямая y=x - касательная к графику функции f(x) = arcsin x в точке перегиба x₀=0, то есть графики пересекаются только в этой точке.
ответ : уравнение имеет единственный корень x=0
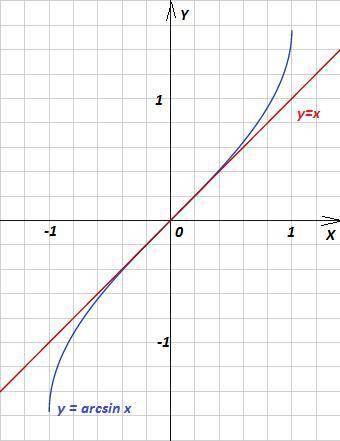
а=5
Решение системы х=2,8
у= -1
Объяснение:
1)ax+3y=11 x= 4 и y= −3
а*4+3*(-3)=11
4а-9=11
4а=11+9
4а=20
а=5
2)Построить графики и найти графически решение системы уравнений.
5x+3y=11
5x+2y=12
Преобразуем уравнения в более удобный для вычислений вид:
5x+3y=11 5x+2y=12
3у=11-5х 2у=12-5х
у=(11-5х)/3 у=(12-5х)/2
Графики линейной функции, прямые линии. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
Таблицы:
у=(11-5х)/3 у=(12-5х)/2
х -2 1 4 х -2 0 2
у 7 2 -3 у 11 6 1
Координаты точки пересечения графиков (2,8; -1)
Решение х=2,8
у= -1
Объяснение:
1. Так как основание степенной функции строго больше нуля, то область определения: х ∈ (0;+∞)
2. Поскольку на ноль деление невозможно, то условие на х: х≠0, а это и есть область определения