1. а) - 4, 5
б) - 1, 2, 4, 5
в) - таких функций нет
2. А - 2
B - 3
C - 1
D - нет подходящего рисунка
3. а) - любые числа
б) x не равно 8, значит принадлежит (-бесконечность;8)U(8;+бесконечность)
4. y = 2.5x-1
т.к. функция линейная, нам нужно найти значение лишь при минимуме и максимуме отрезка -4≤x≤8
y = -4*2.5-1=-11
y=2.5*8-1=19
значит область значений принадлежит [-11;19]
5. точка пересечения: 1;5
Объяснение:
1) || - параллельнсть
l - переменная
k - коэффициент
функции ||, если они не могут быть равны, т.е. у них нет точек пересечения, согласно определению параллельности (|| те прямые, которые не имеют точек пересечения).
а если точка пересечения есть, тогда функции пересекаются, т.е. они оба пересекают определенную координату, следовательно они должны быть равны между собой
линейные функции :
тогда можно прийти к выводу, что если k1=k2, функции параллельны, ибо:
y=kx+l если представить как равно значение:
kx+l=kx+l
l=l, т.е. если k1=k2, l1=l2, проще говоря, не существует какой-либо функции, которая пересекает y=kx+l, если их k равны.
например, y=5x+2
5x+2=5x+2
2=2, если вместо 2 мы подставим любое другое число, равенство станет неверным.
из этого можно сделать вывод, что если k1 не равно k2, тогда функции пересекаются, ибо:
y=k1x + l и y=k2x+l
k1x + l = k2x+ l
l мы сможем сократить только при условии, что они равны, но тогда мы получим все равно верное равенство, просто тогда точкой пересечения будет (0; l), т.е. при x=0 функции станут равными, ибо при умножении k на 0 будет 0, останется только l=l
если же l1 не равно l2, тогда у нас выйдет уравнение с 2 переменными, а значит оно имеет бесконечное множество решений при любом х (если, конечно, x имеет смысл и нет всяких делений на 0 и т.д.), следовательно первая функция при любых значениях k и l будет иметь точку пересечения со второй функцией, если k второй функции не равен k первой функции
2) чтобы установить соответствие, нужно найти минимум 2 значения линейной функции и сравнить результат с графиком.
но чаще всего на рисунках графики будут сильно друг от друга отличаться, поэтому достаточно найти x = 0 и сравнить результат с каждым из рисунков
5) чтобы нарисовать график линейной функции, достаточно найти 2 ее значения (желательно брать максимально простые числа, например, при х 0 и 1), затем проводим линию между этими двумя точками, получив их точку пересечения.
в данном задании можно уравнения представить как линейные функции.
тогда их точка пересечения будет ответом.
Дана функция 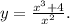
Производная её равна: y' = (3x^2*x^2 - 2x*(x^3 + 4))/x^4 = (x^3 - 8)/x^3.
Приравняем её нулю ( при х не равном 0 можно только числитель).
x^3 - 8 = 0.
x^3 = 8, х = ∛8 = 2. Это критическая точка.
С учётом разрыва функции при х = 0 имеем 3 промежутка монотонности функции: (-∞; 0), (0; 2) и (2; +∞).
На промежутках находим знаки производной.
Находится производная, приравнивается к 0, найденные точки выставляются на числовой прямой; к ним добавляются те точки, в которых производная не определена.
Где производная положительна - функция возрастает, где отрицательна - там убывает. Точки, в которых происходит смена знака и есть точки экстремума - где производная с плюса меняется на минус - точка максимума, а где с минуса на плюс - точки минимума.
x = -1 0 1 2 3
y' = 9 - -7 0 0,7037.
• Минимум функции в точке: х = 2, у = 3.
• Максимума функции нет.
• Возрастает на промежутках: (-∞; 0) U (2; ∞).
• Убывает на промежутке: (0; 2).
координаты вершины параболу (-2 ;-3)