Решите , 45 за полный ответ(+с пояснениями)

👇

Ответ:

УЕД

22.10.2020

$1)\; \; y=\frac{1}{x^2-7x+6}\; \; \to \; \; y=\frac{1}{(x-1)(x-6)} \; \; ,\; \; x\ne 1\; ,\; x\ne 6\\\\D(y)=(-\infty ,1)\cup(1,6)\cup (6,+\infty )\\\\b)\; \; y=\sqrt[5]{1-7x}\; \; ,\; \; D(y)=R\\\\c)\; \; y=\sqrt[6]{x^2-121}\; \; \to \; \; \; y=\sqrt[6]{(x-11)(x+11)}\; \; ,\; \; (x-11)(x+11)\geq 0\; ,\\\\D(y)=(-\infty ,-11]\cup [11,+\infty )\\\\d)\; \; y=2\, cos3x\; \; ,\; \; D(y)=R\\\\e)\; \; y=log_2(9x^2-3x)\; \; ,\; \; 9x^2-3x0\; \; ,\; \; 3x(3x-1)0\; ,\\\\znaki:\; \; \; +++(0)---(\frac{1}{3})+++\\\\D(y)=(-\infty ,0)\cup(\frac{1}{3},+\infty )$

$2)\; \; y=3x+5\; \; \to \; \; 3x=y-5\; ,\; x=\frac{1}{3}\, y-\frac{5}{3}\\\\y=\frac{1}{3}\, x-\frac{5}{3}\\\\b)\; \; y=\frac{2}{3x-1}\; \; \to \; \; 3x-1=\frac{y}{2}\; \; ,\; \; 3x=\frac{y}{2}+1\; ,\; \; x=\frac{y}{6}+\frac{1}{3} \\\\y=\frac{x}{6}+\frac{1}{3}\\\\c)\; \; y=\sqrt[4]{x}+6\; \; \to \; \; \sqrt[4]{x}=y-6\; \; ,\; \; x=(y-6)^4\\\\y=(x-6)^4\\\\d)\; \; y=\frac{1}{2}\, x-6\; \; \to \; \; x=2(y+6)\\\\y=2(x+6)\; \; ,\; \; y=2x+12\\\\e)\; \; 3y=\sqrt[3]{2x}-1\; \; \to \; \; \sqrt[3]{2x}=3y+1\; \; ,\; \; 2x=(3y+1)^3\; ,\; \; x=\frac{1}{2}\, (3y+1)^3\\\\y=\frac{1}{2}\, (3x+1)^3$

4,5(89 оценок)

Открыть все ответы

Ответ:

xayalaamirova2

22.10.2020

Х² + 9х = 0

I.Рациональный решения.

Вынести общий множитель за скобку:

х * (х + 9 ) = 0

Произведение = 0 , если один из множителей =0.

х₁= 0

х + 9=0

х₂= -9

II. Решение через дискриминант [ D= b² -4ac ]

Стандартный вид квадратного уравнения:

х² + 9х + 0 =0

а = 1 ; b= 9 ; с = 0

D = 9² - 4*1*0 = 9²

D>0 - два корня уравнения [ х₁,₂ = (-b ⁺₋ √D)/2a ) ]

х₁ = ( - 9 + √9²) /(2*1) = (-9 + 9)/2 = 0/2 = 0

x₂ = ( - 9 - √9²) /(2*1) = (-9 - 9)/2 = -18/2 = - 9

ответ: ( - 9 ; 0 ) .

Объяснение:

4,7(64 оценок)

Ответ:

shevelevaalla

22.10.2020

$p(x)=a_{1}x^4+a_{2}x^3+a_{3}x^2+a_{4}x+a_{5}\\
 x=\sqrt{x_{1}}\\
 x=\sqrt{x_{1}}+b\\
 x=\sqrt{x_{1}}+2b\\
 x=\sqrt{x_{1}}+3b\\\\
 p(x)+a=a_{1}x^4+a_{2}x^3+a_{3}x^2 + a_{4}x+a_{5}+a\\
y=\sqrt{y_{1}}\\
y=\sqrt{y_{2}}\\
y=\sqrt{y_{3}}\\
y=\sqrt{y_{4}}\\\\ 


$

По теореме Виета для уравнение четвертой степени получаем соотношение
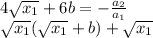
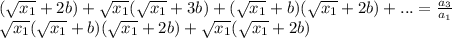
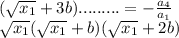
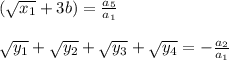
$4\sqrt{x_{1}}+6b = -\frac{a_{2}}{a_{1}}\\ \sqrt{x_{1}}(\sqrt{x_{1}}+b)+\sqrt{x_{1}}$ $(\sqrt{x_{1}}+2b)+\sqrt{x_{1}}(\sqrt{x_{1}}+3b)+(\sqrt{x_{1}}+b)(\sqrt{x_{1}}+2b)+...=\frac{a_{3}}{a_{1}}\\ \sqrt{x_{1}}(\sqrt{x_{1}}+b)(\sqrt{x_{1}}+2b)+\sqrt{x_{1}}(\sqrt{x_{1}}+2b)$ $(\sqrt{x_{1}}+3b).........=-\frac{a_{4}}{a_{1}} \\ \sqrt{x_{1}}(\sqrt{x_{1}}+b)(\sqrt{x_{1}}+2b)$ $(\sqrt{x_{1}}+3b)=\frac{a_{5}}{a_{1}}\\\\ \sqrt{y_{1}}+\sqrt{y_{2}}+\sqrt{y_{3}}+\sqrt{y_{4}}=-\frac{a_{2}}{a_{1}}\\$
\sqrt{y_{1}y_{2}}+\sqrt{y_{1}y_{3}}+\sqrt{y_{1}y_{4}}+\sqrt{y_{2}y_{3}}...+ = \frac{a_{3}}{a_{1}} \\ \sqrt{y_{1}y_{2}y_{3}}+\sqrt{y_{1}y_{2}y_{4}} [/tex]

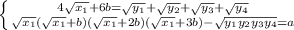
$\left \{ {{4\sqrt{x_{1}}+6b=\sqrt{y_{1}}+\sqrt{y_{2}}+\sqrt{y_{3}}+\sqrt{y_{4}}
 } \atop {\sqrt{x_{1}}(\sqrt{x_{1}}+b)(\sqrt{x_{1}}+2b)(\sqrt{x_{1}}+3b)-\sqrt{y_{1}y_{2}y_{3}y_{4}}=a} \right. \\
$
Учитывая условия что коэффициенты все выражаются в радикалах , то сумма всех корней выраженные в радикалах есть число радикальное .
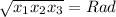По третьем равенству первой системы $\sqrt{x_{1}x_{2}x_{3}}=Rad$ , то произведение корней так же число радикальное , откуда с последних двух идет верное равенство