Решение задания приложено

xy+x+y=11; {xy+x+y=11;
{x²y+xy²=30. ⇒ {xy(x+y)=30.
Пусть х+у=u; xy=v
{v+u=11;
{vu=30.
Решаем систему подстановки:
{v=11-u;
{(11-u)u=30.
Решаем второе уравнение системы
u²-11u+30=0
D=(-11)²-4·30=121-120=1
u₁=(11-1)/2=5 или u₂=(11+1)/2=6
v₁=11-u₁=11-5=6 или v₂=11-6=5
Обратная замена
{x+y=5 или {x+y=6
{xy=6 {xy=5
{y=5-x {y=6-x
{x(5-x)=6 {x(6-x)=5
Решаем вторые уравнения систем:
x²-5x+6=0 x²-6x+5=0
D=25-24=1 D=36-20=16
x₁=(5-1)/2=2; x₂=(5+1)/2=3 x₃=(6-4)/2=1; x₄=(6+4)/2=5
y₁=5-2=3; y₂=5-3=2 y₃=6-1=5; y₄=6-5=1
О т в е т. (2;3) (3;2) (1;5) (5;1).
(a + b)^4 = a^4 + 4a^3b + 6a^2b^2 + 4ab^3 + b^4
(a - b)^4 = a^4 - 4a^3b + 6a^2b^2 - 4ab^3 + b^4
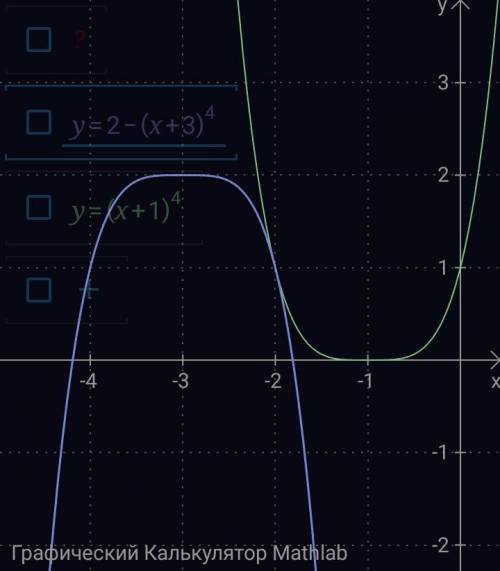
(x+1)^4+(x+3)^4=2
можно сразу возводить в степень, а можно сделать небольшую замену и много что сократится
x + 2 = y
x = y - 2
(y - 1)^4 + (y + 1)^4 = 2
y^4 - 4y^3 + 6y^2 - 4y + 1 + y^4 + 4y^3 + 6y^2 + 4y + 1 = 2
2y^4 + 12y^2 = 0
2y^2(y^2 + 6) = 0
y = 0
x = y - 2 = -2
(y^2 + 6 = 0 не имеет решения в действительных числах, в комплексных решение y = +-i√6 x = -2 +- i√6)
ответ -2