Пусть Х км/ч - скорость 1-го велосипедиста
тогда У км/ч - скорость 2-го велосипедиста
2х - проехал 1-й за 2 ч
2у - приехал 2-й за 2 ч
Известно, что 1-й за 2 ч проехал на 6 км больше
Составим первое уравнение :
2х-2у=6
48/Х - время 1-го велосипедиста
48/у - время 2-го велосипедиста
Известно, что 2-й затратил больше на 32 мин
Выразим минуты в часах :
32 мин = 32/60ч = 8/15 ч
Составим 2-е уравнение:
48/у - 48/Х =8/15
Составим систему уравнений:
{ 2х-2у=6
{ 48/у -48/Х=8/15
2х-2у=6
2х=6+2у
Х= 3+у
48/у - 48/ (3+у) = 8/15
48*15 *(3+у) - 48*15 *у =8у(у+3)
2160 +720 у - 720 у = 8у^2 + 24 у
- 8у^2 -24 у +2160 =0 | : ( -8)
У^2 + 3у - 270 =0
Д= \| 1089=33
У1= ( -3+33)/2 = 15 км/ч
У2= ( -3-33)/2= - 18 км/ч ( не явл корнем )
Х1= 3+у1
Х1= 3+15=18 км/ч
ответ: скорость 1-го велосипедиста 18 км/ч ;
скорость 2-го велосипедиста 15 км/ч
В решении
Объяснение:
1) (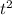 +g)(0,4t-0,7g)
+g)(0,4t-0,7g)
2)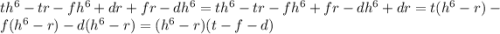
3)56am+32mu-32au-56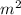 =56am-56
=56am-56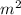 +32mu-32au=56m(a-m)-32u(a-m)=(a-m)(56m-32u)
+32mu-32au=56m(a-m)-32u(a-m)=(a-m)(56m-32u)
4)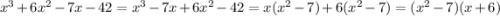
5)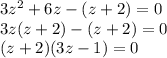
Распадающиеся уравнение