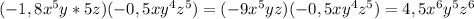
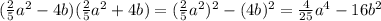
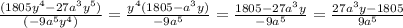
ужас как долго решала, но получилось!
км у нас -гипотенуза треугольника klm
По теореме пифагора :km^2=kl^2+ml^2 (1)
Но kl тоже гипотенуза, но уже треугольника lkp
kl^2=lp^2+kp^2 (2)
подставляем в (1) вместо kl^2 формулу 2
Получаем: km^2= Lp^2+KP^2+ML^2
Переносим lp^2 в одну сторону, а все остальное- в другую :
lp^2=Km^2-kp^2-ML^2 (3)
Еще с другой стороны km у нас это kp+pm
Подставляем это в формулу 3 вместо km и возводим в квадрат, т.к km у нас в квадрате, получаем:(Kp+pm)^2-kp^2-ml^2=lp^2
Раскрываем скобку по формуле, все остальное переписываем
KP^2+2kP*mp+PM^2-kp^2-Ml^=LP^2.(4) То , что я подсеркнула взаимно уничтожается
pm- катет треугольника lpm
По теореме пифагора Pm^2=lm^2-Lp^2 Подставляем это выражение в формулу (4)
вместо Pm^2, получаем:
2Kp*mp+lm^2-lp^2-Ml^2=lp^2 Подчеркнутое взаимно уничтожается, преносим из лвой части в правую lm^2, получаем:2kp*mp=2lp^2 Делим уравнение на 2, поучаем:LP*( в квадрате)=KP*MP
чтд
Пусть дано квадратное уравнение a•x²+b•x+c=0, a≠0. Теорема Виета доказывается для приведённых квадратных уравнений, то есть когда коэффициент a=1. А другие уравнения приводятся к такому виду.
Теорема Виета. Числа x₁ и x₂ являются корнями квадратного уравнения x²+p•x+q=0 тогда и только тогда, когда пара (x₁; x₂) является решением системы:
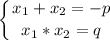
Теорема Виета утверждает, что квадратное уравнение и система одновременно разрешимы или неразрешимы. Ещё, теорема Виета даёт подбора корней:
Корни уравнения являются делителями свободного члена q!
Отсюда вывод: если корни уравнения целочисленные, то легко определить корни, если разложить свободный член q на множители.
Рассмотрим примеры.
Пример-1. Решить уравнение: x²–3•x+2=0.
Решение. По теореме Виета x₁ + x₂ = 3 и x₁ · x₂ = 2. Предполагая, что корни уравнения целочисленные рассмотрим разложение: 2 = 1•2 = (–1)•(–2). Но из x₁ + x₂ = 3 видно, что корнями уравнения будут x₁=1 и x₂=2.
Пример-2. Решить уравнение: x²–6•x+8=0.
Решение. По теореме Виета x₁ + x₂ = 6 и x₁ · x₂ = 8. Предполагая, что корни уравнения целочисленные рассмотрим разложение: 8 = 1•8 = 2•4 = (–1)•(–8) = (–2)•(–4). Но из x₁ + x₂ = 6 видно, что корнями уравнения будут x₁=2 и x₂=4.
Пример-3. Решить уравнение: x²+4•x+4=0.
Решение. По теореме Виета x₁ + x₂ = –4 и x₁ · x₂ = 4. Предполагая, что корни уравнения целочисленные рассмотрим разложение: 4 = 1•4 = 2•2 = (–1)•(–4) = (–2)•(–2). Но из x₁ + x₂ = –4 видно, что корнями уравнения будут x₁= –2 и x₂= –2.
Вот основная суть теоремы Виета.
ответ: 8х³у⁴/45z⁴ * 63z²/16x⁵y³ = x³y⁴*7z² / 5z⁴2x⁵y³ = 7y / 10z²x²
(а²-16в²)/(9а-15в) * (3а-5в)/(4в-а) = (а²-(4в)²)/(3(3а-5в)) * (3а-5в)/(4в-а) = ((а-4в)(а+4в))/(3(4в-а)) = ((а-4в)(а+4в))/(-3(а-4в)) =-(а+4в) / 3
Подробнее - на -
Объяснение: