2
Объяснение:
1-й Угадываем x=2 (проверка: 4=4). Поскольку левая часть возрастает, а правая постоянна, других решений нет.
2-й 

Проверка: 1+3=4 - верно.
3-й Стандартный с двойным возведением в квадрат самый муторный. Надеюсь, что автор второго решения приведет именно его. А меня увольте.
4-й Угадываем x=2: 1+3=4. Преобразуем уравнение к виду
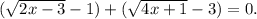
Каждую скобку домножим и разделим на сопряженную к ней (очевидно, что сопряженные выражения не равны нулю):
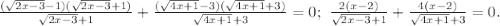
Поскольку x=2 мы уже угадали, можем теперь считать, что  и сократить на (x-2). Получим
и сократить на (x-2). Получим
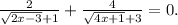
Поскольку левая часть положительна, а правая равна нулю, это уравнение решений не имеет.
Объяснение:
обы доказать неравенство (x - 2)^2 > x(x - 4) выполним тождественные преобразования.
Первым шагом откроем скобки в обеих частях неравенства.
Для открытия скобок будем использовать формулу сокращенного умножения квадрат разности (a - b)^2 = a^2 - 2ab + b^2 и распределительный закон умножения относительно вычитания a * (b - c) = a * b - a * c.
Открываем скобки:
x^2 - 4x + 4 > x^2 - 4x;
Перенесем в левую часть уравнения все слагаемые из правой и приведем подобные слагаемые.
x^2 - x^2 - 4x + 4x + 4 > 0;
4 > 0.
Неравенство верно. Ч. т. д.
Объяснение:
1)
IACI²=17²-8²=289-64=225
IACI=15
sinα=8/17
cosα=IACI/17=15/17
tgα=8/IACI=8/15
sinβ=IACI/17=15/17
cosβ=8/17
tgβ=IACI/8=15/8
2)
IABI²=21²+20²=441-400=841
IABI=29
sinα=21/IABI=21/29
cosα=20/IABI=20/19
tgα=21/20
sinβ=20/IABI=20/29
cosβ=21/IABI=21/29
tgβ=20/21
3)
IABI²=1²+2²=1+4=5
IAB=√5
sinα=1/IABI=1/√5=√5/5
cosα=2/IABI=2/V5=2V5/5
tgα=1/2
sinβ=2/AB=2/√5=2√5/5
cosβ=1/AB=1/√5=√5/5
tgβ=2/1=2
4)
IBCI²=25²-24²=265-576=49
IBCI=7
sinα=IBCI/25=7/25
cosα=24/25
tgα=IBCI/24=7/24
sinβ=24/25
cosβ=IBCI/25=7/25
tgβ=24/IBCI=24/7