1.
a)
x² + 4x + 10 ≥ 0
Рассмотрим функцию у = x² + 4x + 10.
Функция квадратичная, график - парабола, ветви направлены вверх.
Нули функции:
x² + 4x + 10 = 0
D = 16 - 40 = - 24 < 0
нулей нет, значит график не пересекает ось Ох.
Схематически график изображен на рис. 1.
у > 0 при x ∈ (- ∞; + ∞)
ответ: 2) Решением неравенства является вся числовая прямая.
b)
- x² + 10x - 25 > 0 | · (- 1)
x² - 10x + 25 < 0
Рассмотрим функцию у = x² - 10x + 25.
Функция квадратичная, график - парабола, ветви направлены вверх.
Нули функции:
x² - 10x + 25 = 0
(x - 5)² = 0
x = 5
Схематически график изображен на рис. 2.
у < 0 при x ∈ {∅}
ответ: 1) Неравенство не имеет решений.
c)
x² + 3x + 2 ≤ 0
Рассмотрим функцию у = x² + 3x + 2.
Функция квадратичная, график - парабола, ветви направлены вверх.
Нули функции:
x² + 3x + 2 = 0
D = 9 - 8 = 1
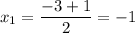
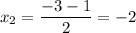
Схематически график изображен на рис. 3.
у ≤ 0 при x ∈ [- 2; - 1]
ответ: 4) Решением неравенства является закрытый промежуток.
d)
- x² + 4 < 0 | · (- 1)
x² - 4 > 0
Рассмотрим функцию у = x² - 4.
Функция квадратичная, график - парабола, ветви направлены вверх.
Нули функции:
x² - 4 = 0
x² = 4
x = ± 2
Схематически график изображен на рис. 4.
у > 0 при x ∈ (- ∞; - 2) ∪ (2; + ∞)
ответ: 6) Решением неравенства является объединение двух промежутков.
___________________________
2.
(x - a)(2x - 1)(x + b) > 0
x ∈(- 4; 1/2) ∪ (5; + ∞)
Решение неравенства показано на рис. 5.
Найдем нули функции у = (x - a)(2x - 1)(x + b).
(x - a)(2x - 1)(x + b) = 0
(x - a) = 0 или (2x - 1) = 0 или (x + b) = 0
x = a x = 1/2 x = - b
Из решения неравенства следует, что нулями являются числа - 4, 1/2 и 5. Значит
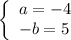 или
или 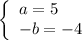
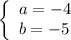 или
или 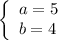
ответ: a = - 4, b = - 5 или a = 5, b = 4.
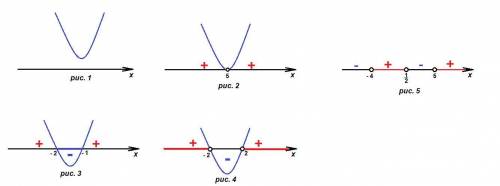
1)10 (км/час) - скорость на велосипеде.
2)8 (см) - длина основания;
10 (см) - длина боковой стороны.
Объяснение:
1. Турист преодолел расстояние в 29 км. 2 часа он ехал на велосипеде,
затем 3 часа шёл пешком. Скорость на велосипеде больше скорости
пешком на 7 км. Найти скорость движения на велосипеде.
х - скорость пешком
х+7 - скорость на велосипеде
3*х - путь пешком
(х+7)*2 - путь на велосипеде
По условию задачи весь путь 29 км, уравнение:
3х+2(х+7)=29
3х+2х+14=29
5х=29-14
5х=15
х=15/5
х=3 (км/час) - скорость пешком
3+7=10 (км/час) - скорость на велосипеде.
2 Периметр равнобедренного треугольника 28 см. Боковая сторона
на 2 см больше основания . Найти стороны РАВНОБЕДРЕННОГО
треугольника.
х - длина основания
х+2 - длина боковой стороны
Периметр треугольника - это сумма длин всех сторон треугольника. Так как треугольник равнобедренный, в нём боковые стороны равны.
По условию задачи периметр треугольника 28 см, уравнение:
х+2(х+2)=28
х+2х+4=28
3х=28-4
3х=24
х=24/3
х=8 (см) - длина основания
8+2=10 (см) - длина боковой стороны.
решение смотри на фотографии
Объяснение: