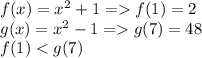
ответ: -((4a/(a+3)).
Объяснение: ((9a-13)/(a²-9) - (5a²+15a+45)/(a³-27)) ÷ ((a-7)/(3a-a²))=
=((9a-13)/(a²-9) - ((5×(a²+3a+9))/(a³-3³)) ÷ ((a-7)/(3a-a²)) =
=((9a-13)/((a-3)×(a+3)) - ((5×( a²+3a+9))/((a-3)×(a²+3a+9))) ÷
÷ ((a-7)/(3a-a²))=
=((9a-13)/((a-3)×(a+3)) - (5/(a-3))) ÷ ((a-7)/(3a-a²))=
=((9a-13-5×(a-3))/((a-3)×(a+3))) ÷ ((a-7)/(3a-a²)) =
=((9a-13-5a-15)/((a-3)×(a+3))) ÷ ((a-7)/(3a-a²)) =
= ((4a-28)/((a-3)×(a+3))) ÷ ((a-7)/(3a-a²)) =
= ((4a-28)/((a-3)×(a+3)) × ((3a-a²)/(a-7)) =
= (4×(a-7)×a×(3-a))/((a-3)×(a+3)×(a-7))= ((4a×(3-a))/((a-3)×(a+3))=
= (-4a×(a-3))/((a-3)×(a+3)) = -((4a)/(a+3)).
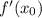производная функции в данной точке. А 
точка касания по иксу.
мы должны найти производную общего типа этой функции.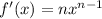
- где n это степень.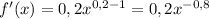
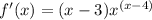
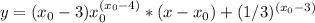
и получаешь уравнение касательной.
f(1)<g(7)
Объяснение:
f(x)=x²+1 f(1)=1²+1=2
g(x)=x²-1 g(7)=7²-1=49-1=48