Здравствуйте, Sonya2006f!
Чтобы восстановить неполный квадрат суммы, нужно представить крайние члены данной формулы в виде числа со степенью.
Разложение чисел на простые множители:
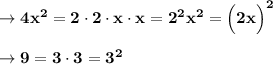
Теперь когда мы знаем, как представить данные члены в виде числа со степенью, запишем формулу, по которой выполнялось разложение.
Формула сокращённого умножения:
НЕПОЛНЫЙ КВАДРАТ СУММЫ: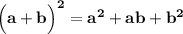 
.
Зная, что первоначально выражение имело вид 
, перемножим по формуле эти члены между собой и получим ответ на Ваш вопрос.
Разложение данного выражения на множители:
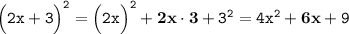
Окончательный ответ данной задачи:
Неполный квадрат суммы данного выражения - "6x".
С Уважением, NeNs07.
n^46:n^41=n^5
при делении степени вычитаются