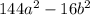1. (7-3а)(7+3а)=14-21а-21а-9а=14-9а
2.(7а4+11b)(7a4-11b)=хз как записать
3.(12а-4b)(12a+4b)=.наподобие первому, чем смог тем
Напомним, по определению корня четной степени он всегда больше равен 0. 1 - x ≥ 0 x ≤ 1
ОДЗ , подкоренное выражение должно быть больше равно 0 . находить его сейчас не будем, проверим корни когда их найдем
тупо возводим в квадрат
x^3 + 2x^2 - 6x - 3 = (1 - x)^2
x^3 + 2x^2 - 6x - 3 = 1 -2x + x^2
x^3 + x^2 -4x - 4 = 0
x^2(x + 1) - 4(x + 1) = 0
(x + 1)(x^2 - 4) = 0
(x+1)(x+2)(x-2) = 0
x = -1 проверяем поодкоренное выражение оно должно быть ≥ 0 -1 + 2 + 6 - 3 = 4 > 0 да подходит
x = 2 нет , у нас ограничения x ≤ 1
x = -2 -8+8+12-3 = 9 > 0 да подходит
корни -1 и -2
11 в любой степени кончается на 1. 19 в нечетной степени кончается на 9.
Их сумма кончается на 1+9=10, то есть на 0, а значит, делится на 5.
Осталось доказать, что это число делится на 3.
11=3*3+2; 11^2019 = (3*3+2)^2019 = 2^2019.
Здесь и дальше знак = означает "такой же остаток при делении на 3".
2^2019 = (2^3)^673 = 8^673 = 2^673 = 2^3*2^670 = 8*(2^10)^67 = 2*1024^67 =
= 2*(3*341+1)^67 = 2*1^67 = 2
Таким образом, 11^2019 имеет при делении на 3 остаток 2.
19 = 3*6+1; 19^2019 = (3*6+1)^2019 = 1^2019 = 1.
Таким образом, 19^2019 имеет при делении на 3 остаток 1.
Сумма этих чисел имеет остаток 2+1=3, то есть делится нацело.
Что и требовалось доказать.
Объяснение:
Тут можно заметить что в конце получается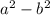
1)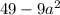
2)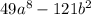
3)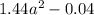
4)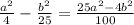
5)