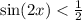
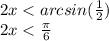
разделим обе стороны на 2 чтоб упростить
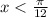
Функция синуса принимает положительные значения в первом и втором квадрантах. Для определения второго решения вычитаем решение из
π
, чтобы найти решение во втором квадранте.
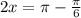
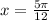
Период функции
sin(2х)
равен
π
, то есть значения будут повторяться через каждые
π
радиан в обоих направлениях
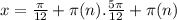
для всех целых n
Выбираем тестовое значение из каждого интервала и подставляем его в начальное неравенство, чтобы определить, какие интервалы удовлетворяют неравенству.
1.
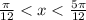
1 это ложно
2.
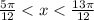
2 это истинно
3.
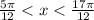
3 это ложно.
Итак
решение включает все истинные интервалы:
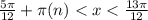
для всех целых n
разделим обе стороны на 2 чтоб упростить
Функция синуса принимает положительные значения в первом и втором квадрантах. Для определения второго решения вычитаем решение из
π
, чтобы найти решение во втором квадранте.
Период функции
sin(2х)
равен
π
, то есть значения будут повторяться через каждые
π
радиан в обоих направлениях
для всех целых n
Выбираем тестовое значение из каждого интервала и подставляем его в начальное неравенство, чтобы определить, какие интервалы удовлетворяют неравенству.
1.
1 это ложно
2.
2 это истинно
3.
3 это ложно.
Итак
решение включает все истинные интервалы:
для всех целых n