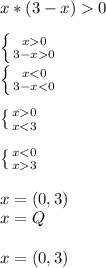
используя формулу квадрата суммы или квадрата разности двух выражений,вычислите 1)101 в квадрате=(100+1) в квадрате,2)31 в квадрате,3) 51 в квадрате,4)39 в квадрате,5)103 в квадрате,6)99 в квадрате,7)999 в квадрате,8)1001 в квадрате,9)105 в квадрате,10)52 в квадрате.
Поскольку для любых действительных чисел справедливы выражения: (a+b)^2 = (a+b)(a+b) = a^2+2ab+b^2 (формула квадрата суммы) и (a-b)^2 = (a-b)(a-b) = a^2-2ab+b^2 (формула квадрата разности), то решение для данных примеров:
1) 101^2 = (100+1)^2 = 100^2+2×100×1+1^2 = 10000+200+1 = 10201,
2) 31^2 = (30+1)^2 = 30^2+2×30×1+1^2 = 900+60+1 = 961,
3) 51^2 = (50+1)^2 = 50^2+2×50×1+1^2 = 2500+100+1 = 2601,
4) 39^2 = (40-1)^2 = 40^2-2×40×1+1^2 = 1600-80+1 = 1521,
5) 103^2 = (100+3)^2 = 100^2+2×100×3+3^2 = 10000+600+9 = 10609,
6) 99^2 = (100-1)^2 = 100^2-2×100×1+1^2 = 10000-200+1 = 9801,
7) 999^2 = (1000-1)^2 = 1000^2-2×1000×1+1^2 = 1000000-2000+1 = 998001,
8) 1001^2 = (1000+1)^2 = 1000^2+2×1000×1+1^2 = 1000000+2000+1 = 1002001,
9) 105^2 = (100+5)^2 = 100^2+2×100×5+5^2 = 10000+1000+25 = 11025,
10) 52^2 = (50+2)^2 = 50^2+2×50×2+2^2 = 2500+200+4 = 2704.
попробую дать более подробный разбор
итак дано неравентсво
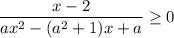 . где a>0
. где a>0
рассмотрим знаменатель дроби
зададим функцию f(x)=ax²-(a²+1)x+a; т.к. a>0 то это парабола, ветви "вверх"
найдем ее корни
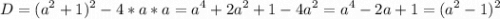
тогда
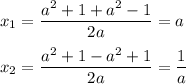
а теперь рассуждения:
чтобы решить неравентсво методом интервалов определяем корни числителя и знаменателя, это числа 2, a и 1/а
1) все корни различны
напомню что а и 1/а корни параболы "ветви вверх" , х=2 корень прямой направленной тоже вверх. Тогда не проблема расставить знаки промежутков
получим вариант №1
парабола ___+___ 1/а______---_______а___+__
прямая ------- 2 +
и тогда решением будет (1/a;2] ∪ (a;+∞)
увы- не луч.. а отрезок и луч
вариант №2
парабола __+_ 1/а___---__а___+_______
прямая ------- 2 +
и тогда решением будет (1/a;а) ∪ [2;+∞)
увы- не луч.. а отрезок и луч
2) теперь допустим что a=2; тогда 1/a=0.5
рисуем
парабола __+_ 1/а___---__а___+_______
прямая ------- 2 +
и тогда решением будет (1/2;2) ∪ (2;+∞)
т.к. х=2 корень знаменателя и он выкалывается
и опять не луч
аналогично при 1/а=2
3) осталось проверить условие что а=1/а, это возможно при а=1
рисуем
парабола __+_ 1/а=а___+_______
прямая ------- 2 +
и тогда решением будет [2;+∞)
Уряяя. получили просто луч