6x²+12х+6=0
Объяснение:
Раскрываем скобки
9х²+12х+4=10+3х²-12
Переносим в левую часть
9х²+12х+4-10-3х²=0
Приводим подобные слагаемые
6х²+12х+6=0
1 коэффициент равен шести
2 коэффициент равен двенадцати
3 коэффициент (свободный член) равен шести
Объяснение:
1) Треугольники ABM и CBM
AB=BC (по условию)
BM - общая
∠M=90° (по условию)
Вывод: треугольники равны по катету и гипотенузе
2) Треугольники FDN и NKF
DN=FK (по условию)
FN - общая
∠D=∠K=90° (по условию)
Вывод: треугольники равны по катету и гипотенузе
3) Треугольники SDO и SPO
∠D=∠P=90° (по условию)
SO - общая
∠SOD=∠SOP (по условию)
Вывод: треугольники равны по гипотенузе и острому углу
4) Треугольники RMX и XNR
RX - общая
∠MXR=∠NRX (по условию)
∠M=∠N=90° (по условию)
Вывод: треугольники равны по гипотенузе и острому углу
Треугольники MRT и NXT:
RT=XT (тк ∠MXR=∠NRX (по условию), треугольник RTX - равнобедренный (по свойству))
∠M=∠N=90° (по условию)
Из доказательства пары этого пункта ∠MRX=∠NXR (соотв. элементы равных фигур равны), но ∠MXR=∠NRX (по условию)=> ∠MRT=∠NXT
Вывод: треугольники равны по гипотенузе и острому углу
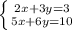
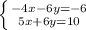
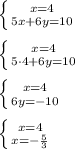
(3x+2 )²=10+3(x-2) (x+2)
9x²+12x+4=10+3(x²-4)
9x²+12x+4=10+3x²-12
9x²+12x+4-10-3x²+12=0
6x²+12x+6=0
старший коэффициент 6
второй коэффициент 12
свободный член 6