5) x=0, x= -2,5
6) f(1)=5
7) 500500
Объяснение:
5) 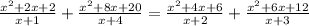
x ≠ -1, x ≠ -2, x ≠ -3, x ≠ -4
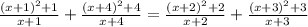
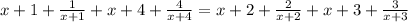
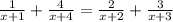
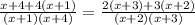
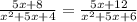
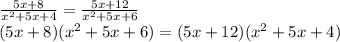
5x³+25x²+30x+8x²+40x+48=5x³+25x²+20x+12x²+60x+48
4x²+10x=0 ⇒ x=0, x= -2,5
6) 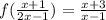
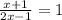
x+1=2x-1 ⇒ x= 2
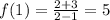
7) 1000·999-998·997+996·995-994·993-...+4·3-2·1
1000·999-998·997=(2+998)·999-998·997=2·999+998·999-998·997=
=2·999+2·998=2·(999+998)
996·995-994·993=(2+994)·995-994·993=2·995+994·995-994·993=
=2·995+2·994=2·(995+994)
...
4·3-2·1=(2+2)·3-2·1=2·3+2·3-2·1=2·3+2·2=2·(3+2)
1000·999-998·997+996·995-994·993-...+4·3-2·1= =2·(999+998)+2·(995+994)+...+2·3+2·2=
=2·(999+995+991+...+3)+2·(998+994+990+...+2)=
=2·(3+999):2·((999-3):4+1)+2·(2+998):2·((998-2):4+1)=
=1002·250+1000·250=250·2002=500500
|x-3|-3≥0
Уравнение примет вид:
|x-3|-3=3-|3-х|
или
2|x-3|=6 (|x-3|=|3-х|- модули противоположных выражений равны)
|x-3|=3
х-3=3 или х-3=-3
х=6 или х=0
х=6 и х=0 являются корнями уравнения, так как удовлетворяют неравенству
|x-3|-3≥0
2)
|x-3|-3<0
Уравнение примет вид:
-|x-3|+3=3-|3-х|
или
|x-3|=|3-х| - равенство верно при любом х.
Корнем уравнения являются те х, которые удовлетворяют неравенству
|x-3|-3<0
или
|x-3|<3
-3<x-3<3
0<x<6
ответ. х=0; х=6; 0<x<6 или 0≤х≤6 или х∈[0;6]