ответ: сори ответила только на первый пример
3
2(1−3x)
+
2
3x−3
=
6
x−3
−1
Умножьте обе стороны уравнения на 6, наименьшее общее кратное чисел 3,2,6.
2×2(1−3x)+3(3x−3)=x−3−6
Перемножьте 2 и 2, чтобы получить 4.
4(1−3x)+3(3x−3)=x−3−6
Чтобы умножить 4 на 1−3x, используйте свойство дистрибутивности.
4−12x+3(3x−3)=x−3−6
Чтобы умножить 3 на 3x−3, используйте свойство дистрибутивности.
4−12x+9x−9=x−3−6
Объедините −12x и 9x, чтобы получить −3x.
4−3x−9=x−3−6
Вычтите 9 из 4, чтобы получить −5.
−5−3x=x−3−6
Вычтите 6 из −3, чтобы получить −9.
−5−3x=x−9
Вычтите x из обеих частей уравнения.
−5−3x−x=−9
Объедините −3x и −x, чтобы получить −4x.
−5−4x=−9
Прибавьте 5 к обеим частям.
−4x=−9+5
Чтобы вычислить −4, сложите −9 и 5.
−4x=−4
Разделите обе части на −4.
x=
−4
−4
Разделите −4 на −4, чтобы получить 1.
x=1
Объяснение:
По формуле:
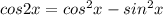
Зная это получаем:
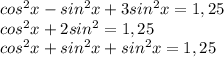
Известно что:
отсюда получаем:
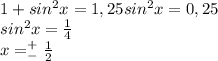
Получаем 2 уравнения:
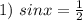это табличное значение синуса и получается 2 решения:
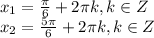
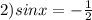аналогично получаем 2 решения:
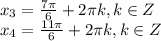
Теперь обратим внимание, что эти 4 решения можно записать в 2 решения в виде:
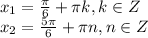
Теперь надо найти при каких значениях k и n решения лежат на отрезке ![[0; \frac{5\pi}{2}]](/tpl/images/0071/0603/9e0ce.png)
Для этого решаем 2 неравенства
1) 
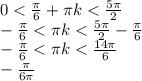
Так как к у нас принадлежит целым числам, то получается что к=0,1,2
2) Теперь ищем n, аналогично:
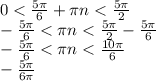
Поскольку n принадлежит целым числам, то получается что n=0,1
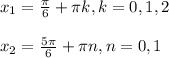
10 в 50 степени минус 4 = 9...96 (49 девяток) это число кратно 3 т. к. его сумма цифр делится на 3
Объяснение: