Пусть одна диагональ равна 2х, другая - 2у, тогда 2х+2у=24 и х+у-12, откуда у=12-х.
Диагонали ромба пересекаются под прямым углом, таким образом, площадь ромба состоит из 4-х прямоугольны треугольников с катетами х и у, т.е. площадь ромба S=4*0.5xy=2xy.
Подставим сюда у=12-х и получим S=24x-2x^2.
Найдём максимум этой функции. S'= 24-4x.
Стационарная точка: 24-4х=0 х=6
При х=7 S'<0; при х=5 S'>0, следовательно при х=5 имеем максимум S.
у=12-х=12-6=6.
Тогда Smax=2*6*6=72.
Интересно, что получился квадрат с диагоналями, равными 12.
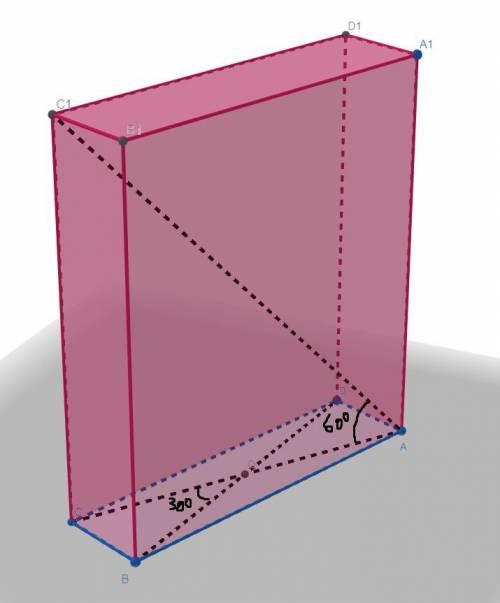
угол между прямой и плоскостью, это угол между прямой и ее проекцией на эту плоскость.
точка C1 проецируется в точку C => отрезок AC1 проецируется в диагональ AC.
угол CAC1=60°
Из треугольника ACC1:
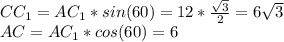
CO=BO из свойств прямоугольника => треугольник COB равнобедренный.
2∠OBC+∠COB=180° (как углы треугольника)
∠OBC=(180-30)/2=75°
Из треугольника DCB, ∠CDB=180°-90°-75°=15°
AC=BD из свойств прямоугольника.
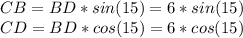
Раскрывать синус и косинус 15 глупо, но это легко можно сделать например как sin(45-30) или sin(60-45) или sin(30/2).
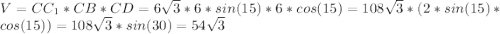
------------------
ответ 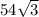
Если что-то непонятно задай вопрос
243=3^5
3*3^(1/5)=3^(1+1/5)=3^(6/5)
25log(243)3^(5/6)=25/5*log(3)3^(6/5)=5*6/5=6
пусть log(3)x=a; x=3^a
(3^a)^a=6-(3^a)^2
3^(a^2)=6-3^(a^2)
2*3^(a^2)=6
3^(a^2)=3
a^2=1; a=+-1
x1=3^1=3
x2=3^(-1)=1/3