xy + x - y = 7 xy + x - y = 7 Замена: xy = а; x - y = b
x²y - xy² = 6 xy(x - y) = 6
a + b = 7
ab = 6 Систему решаем, применив т. Виета.
a₁ = 1 или a₂ = 6
b₁ = 6 b₂ = 1
Обратная замена:
1) xy = 1 или 2) xy = 6
x - y = 6 x - y = 1
Решаем каждую систему совокупности:
1) xy = 1 (6 + y)y = 1; 6y + y² = 1; y² + 6y - 1 = 0;
x = 6 + y y₁ = -3 + √10; y₂ = -3 - √10
x₁ = 3 + √10; x₂ = 3 - √10
(3 + √10; -3 + √10), (3 - √10; -3 - √10).
2) xy = 6 (y + 1)y = 6; y² + y - 6 = 0;
x = y + 1 y₁ = -3; y₂ = 2
x₁ = -2; x₂ = 3
(-3; -2), (3; 2)
ответ: (3 + √10; -3 + √10), (3 - √10; -3 - √10), (-3; -2), (3; 2).
1. Цветных шаров в ящике 5, поэтому вероятность вытащить цветной шар равна  , что равно 0,5.
, что равно 0,5.
ответ: вероятность того, что вынутый наугад шар цветной равна 0,5.
2. Еще раз напишу условие, для удобста: cos 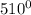 - sin
- sin 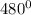 + tg
+ tg 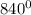 .
.
Рассмотрим каждое слагаемое в отдельности:
cos 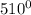 = cos
= cos 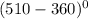 = cos
= cos 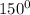 = -
= - 
sin 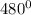 = sin
= sin 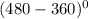 = sin
= sin 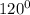 =
= 
tg 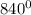 = tg
= tg 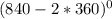 = tg
= tg 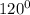 = -
= - 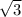
Теперь заменим слагаемые в исходном выражении полученными значениями:
cos 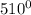 - sin
- sin 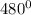 + tg
+ tg 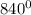 = -
= -  -
-  -
- 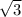 = -2*
= -2*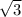
ответ: -2*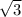
3. В физике уравнение движения точки выглядит следующим образом:
S = 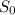 +
+ 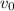 t +
t + 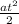
Обратимся теперь к уравнению, данному в условии:
S(t) = 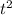 - 8t + 4
- 8t + 4
Заметим, что 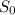 = 4,
= 4, 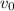 = -8, a = 2.
= -8, a = 2.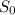
Уравнение изменения скорости:
v = 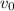 + at
+ at
Подставим в него вместо v - 0, как требуется в условии и вместо 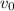 и a найденные нами значения и решим полученное уравнение:
и a найденные нами значения и решим полученное уравнение:
0 = -8 + 2t
8 = 2t
t = 4
ответ: скорость точки окажется равной нулю через 4 единицы времени после начала движения.
4. Формула объема правильного тетраэдра:
V = 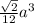 , где a - длина ребра.
, где a - длина ребра.
Пусть ребро данного тетраэдра равно l. Тогда его объем выражается формулой 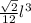 , обозначим его как
, обозначим его как 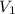 .
.
Ребро же нового тетраэдра равно 4l.
Подставим его в формулу объема, вместо a:
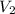 =
= 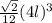 =
= 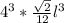 =
=  = 64
= 64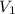
Подставим вместо 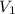 значение, данное в условии:
значение, данное в условии:
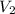 = 64*3 = 192 см
= 64*3 = 192 см
ответ: объем такого правильного тетраэдра равен 192 см
1) Существует бесконечно много квадратов натуральных чисел, представимых в виде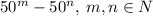 .
.
Для доказательства этого факта достаточно взять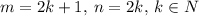 . И правда:
. И правда: 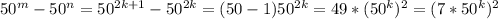
2) Не существует квадратов натуральных чисел, представимых в виде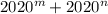 .
.
Для этого рассмотрим остаток от деления выражения на 3: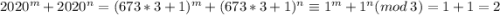
С другой стороны, квадрат натурального числа может давать остатки 1 или 0 при делении на 3. И правда: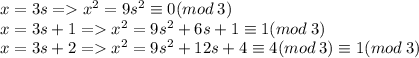
Противоречие.
Ч.т.д.
Использованы свойства сравнения чисел по модулю