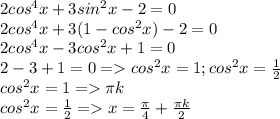
k∈Z
ответ: Минимум (-3;-1). Рост функции на интервале (-3;+∞). Функция убывает на промежутке (-∞;-3)
Объяснение:
Наименьшее значение:
Перед нами уравнение параболы. Известно, что экстремальное значение параболы достигается при 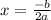 (здесь b - коэффициент при x, а а - коэффициент при x^2)
(здесь b - коэффициент при x, а а - коэффициент при x^2)
Находим x:
x = -3 ⇒ подставляем это значение в функцию ⇒ y = -1 (данный y - минимум, которого может достичь функция)
Точка минимума - (-3;-1)
Промежуток, на котором функция возрастает:
Понятно, что данная парабола ветвями вверх, так как 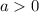 . Значит, функция возрастает после прохождения своего минимума:
. Значит, функция возрастает после прохождения своего минимума:
Рост функции:
x ∈ (-3; +∞)
Промежуток на котором функция убывает:
Функция убывает пока не достигнет своего минимума
Уменьшение функции:
x ∈ (-∞; -3)
ответ: Минимум (-3;-1). Рост функции на интервале (-3;+∞). Функция убывает на промежутке (-∞;-3)
Объяснение:
Наименьшее значение:
Перед нами уравнение параболы. Известно, что экстремальное значение параболы достигается при 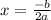 (здесь b - коэффициент при x, а а - коэффициент при x^2)
(здесь b - коэффициент при x, а а - коэффициент при x^2)
Находим x:
x = -3 ⇒ подставляем это значение в функцию ⇒ y = -1 (данный y - минимум, которого может достичь функция)
Точка минимума - (-3;-1)
Промежуток, на котором функция возрастает:
Понятно, что данная парабола ветвями вверх, так как 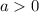 . Значит, функция возрастает после прохождения своего минимума:
. Значит, функция возрастает после прохождения своего минимума:
Рост функции:
x ∈ (-3; +∞)
Промежуток на котором функция убывает:
Функция убывает пока не достигнет своего минимума
Уменьшение функции:
x ∈ (-∞; -3)
Можно было решить пункты а) и b) , не избавляясь от квадратов косинуса, но тогда надо объединять решения.