ОДЗ:
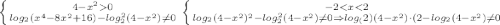
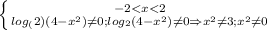
ОДЗ:
x∈(-2;-√3)U(-√3;0)U(0;√3)U(√3;2)
Так как в условиях ОДЗ
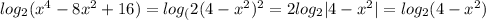
Замена переменной:
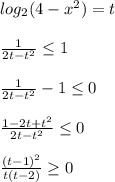
Применяем метод интервалов:
__+__ (0) __-__ [1] __-___(2) __+_
t < 0 или t=1 или t > 2
Обратный переход:
log₂(4-x²) < 0 или log₂(4-x²)=1 или log₂(4-x²)>2
log₂(4-x²) <log₂1 или log₂(4-x²)=log₂2 или log₂(4-x²)>log₂4
Логарифмическая функция с основанием 2 возрастающая, поэтому большему значению функции соответствует меньшее значение аргумента:
4-х²<1 или 4-x²=2 или 4-x²>4
x²>3 или x²=2 или x²<0
С учетом ОДЗ получаем ответ
(-2;-√3)U(√3;2)
1) x²-6x-7=0.
по т. виета:
х1= 7, х2= -1.
ответ: -1; 7.
2) 2х²-3х+1=0;
d= b²-4ac= 9-9=0 => один корень.
х= (3+0)/4= ¾.
ответ: ¾.
3) 5х²+2х-3=0;
d= 4+60=64=8².
x1= (-2+8)/10= 6/10= 0,6
x2= (-2-8)/10= -10/10= -1.
ответ: -1; 0,6.
4) 2х²+5х-7=0;
d= 25+56= 81=9².
x1= (-5+9)/4= 4/4= 1.
x2= (-5-9)/4= -14/4= -7/2= -3½= -3,5.
ответ: -3,5; 1.
5) х²-8х-9=0;
по т. виета:
х1= 9, х2= -1.
ответ: -1; 9.
6) х²-х-2=0;
по т. виета:
х1= 2, х2= -1.
ответ: -1; 2.
7) х²+3х-4=0;
по т. виета:
х1= -4, х2= 1.
ответ: -4; 1.
p.s. все формулы смотреть во вложении, если теорему виета не учили, делаете все по формуле через дискриминант, как это было у меня в половине примеров! есть вопросы -