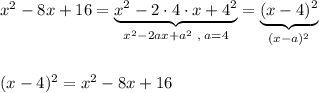
1) 2 * р - 4 * Х = р * Х + 3
(р + 4) * Х = 2 * р - 3
Уравнение не имеет корней, если коэффициент при Х равен 0, а правая часть не равна 0, то есть при р = -4
2) Если модули равны, то подмодульные выражения либо равны, либо противоположны
а) Поскольку уравнение Х - 3,5 = Х + 3,5 корней не имеет, то
Х + 3,5 = -(Х - 3,5) , откуда Х = 0
б) Поскольку уравнение Х - 1 = Х + 3 корней не имеет, то
Х + 3 = -(Х - 1) , откуда Х = -1
в) Если дробь равна 0, то числитель равен знаменателю.
В данном случае |Х|= Х , откуда Х > 0 (вариант Х = 0 не подходит из-за деления на 0)
ответ: 4
Объяснение:
(x - *)² = x² - 2x* + * ²
-2x* = -8x; -2x* = -2 × x · 4 ⇒ * = 4.
Проверка: (x - 4)² = x² - 2 · 4x + 4² = x² - 8x + 16 - то, что нужно.