1. ОТВЕТ: например, 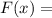
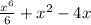 , поскольку
, поскольку 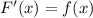 .
.
Общий вид первообразных - 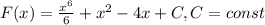
2. Докажем, что 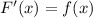 :
:
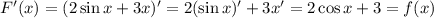 .
.
Что и требовалось доказать.
3. Общий вид первообразных функции 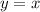 -
- 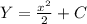 , где
, где 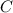 - некоторое постоянное число. Если график первообразной проходит через точку
- некоторое постоянное число. Если график первообразной проходит через точку 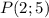 , то это значит, что при подстановке
, то это значит, что при подстановке 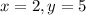 получим верное равенство:
получим верное равенство:
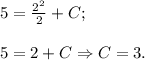
Искомая первообразная - 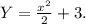
ОТВЕТ: Y = x²/2 + 3.
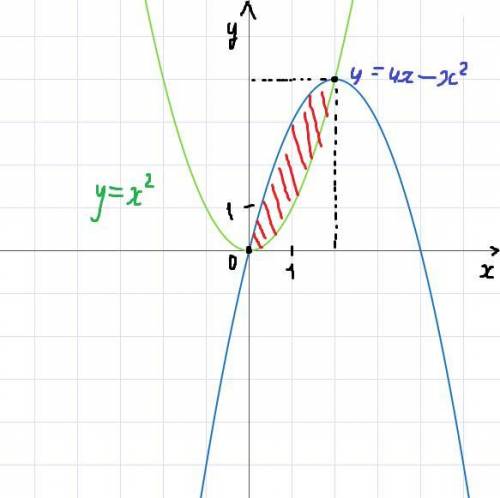
4. Графики функции - во вложении 1. Площадь заданной фигуры заштрихована красным.
Поскольку график функции y = 4x - x² на отрезке [0; 2] располагается как минимум не ниже графика функции y = x² (выполняется неравенство 4x - x² ≥ x²), то площадь будет иметь вид
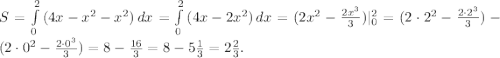
ОТВЕТ: 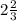 кв. ед.
кв. ед.
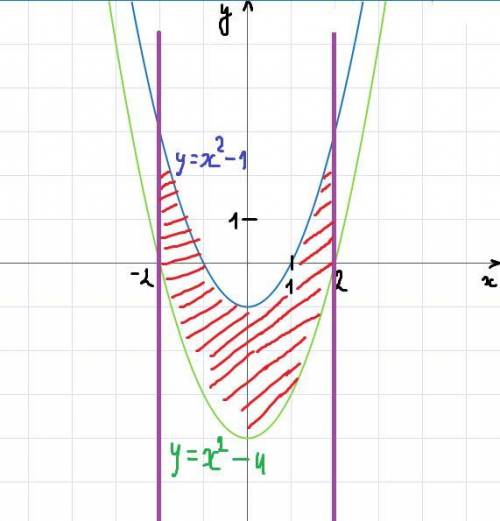
5. Графики - во вложении 2. Площадь заданной фигуры заштрихована красным.
Поскольку на отрезке (-2; 2) график функции y = x² - 1 располагается выше графика функции y = x² - 4 (выполняется равенство x² - 1 > x² - 4), то площадь будет иметь вид
![S=|\int\limits^2_{-2} {[x^2-1-(x^2-4)]} \, dx |=\int\limits^2_{-2} {3} \, dx= (3x)|_{-2}^2=3\cdot2-[3\cdot(-2)]=6+6=12](/tpl/images/1179/2526/6e4c7.png)
ОТВЕТ: 12 кв. ед.
6. Объем выполненной работы A(t) с момента 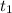 по момент
по момент 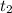 согласно механическому смыслу определенного интеграла есть значение выражения интеграла
согласно механическому смыслу определенного интеграла есть значение выражения интеграла
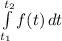
Имеем:
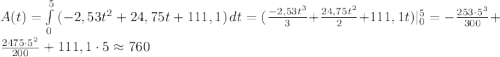
ОТВЕТ: ≈ 760.
ответ: -4
Объяснение:
Поскольку уравнения :
x(x^2-2x-7)-a=0
x(x^2+3x-2)-b=0
имеют два общих корня , то их разность обязана иметь эти два корня.
x(x^2+3x-2)-b - x(x^2-2x-7)+a=0
x*(5x+5)+a-b=0
5x^2+5x+(a-b)=0
x^2+x+(a-b)/5=0
Поскольку это квадратное уравнение , то оно имеет не более двух корней. Cоответственно данное уравнение должно иметь ровно два корня и эти корни как раз являются общими для двух данных уравнений:
x(x^2-2x-7)-a=0
x(x^2+3x-2)-b=0
x^2+x+(a-b)/5=0
По теореме Виета это значит , что сумма этих двух общих корней равна -1.
Вернемся к уравнению 1
x^3-2*x^2-7*x-a=0
Поскольку это уравнение имеет хотя бы два действительных корня , то поскольку это уравнение нечетной степени , то автоматически имеет и 3 действительный корень. (Многочлен нечетной степени всегда имеет нечетное число действительных корней )
Тогда, согласно общей теореме Виета, cумма всех трех корней этого уравнения равна - его второй член .
То есть x1+x2+x3=-(-2)=2
Cумма первых двух нам известна :
x1+x2=-1
Откуда : x3= 2-(-1)=3
Таким образом параметр a, если он существует, единственный и его можно найти просто подставив его 3 корень в уравнение
a= 3*(3^2-2*3-7)= 3*(-4)=-12
Аналогично для уравнения 2 можно получить параметр b
x1+x2+x3=-3
x3=-3-(-1)=-2
b= -2*( 4-6-2)= -2*(-4)=8
Поскольку мы произвели преобразование разности уравнений , то хотя бы для одного из уравнений требуется сделать проверку.
Как мы уже знаем
x^2+x+(a-b)/5=0
x^2+x+(-12-8)/5=0
x^2+x-4=0
Проверим являются ли эти корни корнями уравнения
x^3-2*x^2-7*x+12=0
Для этого выполним произведение (учитывая , что x3=3)
(x^2+x-4)*(x-3)= x^3+x^2-4*x-3*x^2-3*x+12=x^3-2*x^2-7*x+12 -совпадает с исходным.
ответ: a=-12 ; b=8 ; a+b =-4