х³-3х²+(а+2)х-2а=0
х³-3х²+ах+2х-2а=0
х(х²-3х+2)+а(х-2)=0
х((х-2)(х-1))+а(х-2)=0
(х-2)(х(х-1)+а)=0
(х-2)(х²-х+а)=0
1) х-2=0 => х=2
Если уравнение должно иметь 2 противоположных корня, то второй множитель должен иметь один из корней, равный -2:
х²-х+а=0
(х+2)(х-3)=0
х²-х+6=0
Уравнение имеет 3 корня: х=2; х=-2; х=3.
Подставим все значения Х в уравнение:
1) х³-3х²+(а+2)х-2а=0
2³-3×2²+(а+2)×2-2а=0
8-12+2а+4-2а=0
0=0
2) х³-3х²+(а+2)х-2а=0
(-2)³-3×(-2)²+(а+2)×(-2)-2а=0
-8-12-2а-4-2а=0
-4а-24=0
а=-6
3) х³-3х²+(а+2)х-2а=0
3³-3×3²+(а+2)×3-2а=0
27-27+3а+6-2а=0
а=-6
ответ: а=-6
Для доказательство просто рассмотрим два случая: когда
- нечетное и когда 
- четное.
1).
- нечетное, то есть 
.
При всех нечетных натуральных
число 
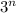имеет остаток 
при делении на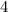 
.
Доказать это можно таким образом: приТакже, при любом натуральном значении
число 
имеет остаток 
при делении на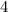 
.
Так происходит, потому что само числоТретье слагаемое: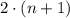
будет нацело делиться на 
:
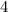Значит, если
- нечетное, то:
При нечетных
все, как видите, сходится.
2).
- четное, или же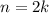 
.
Как мы определили ранее, в этом случае
и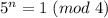 
.
При этом второе слагаемое:
Найдем всю сумму:
И при четных
утверждение работает.
Как известно, каждое натуральное число либо четное, либо нечетное (третьего не дано) и никаких других натуральных чисел, которые не являются четными и не являются нечетными одновременно, науке неизвестно.
Так что мы рассмотрели все случаи, и в каждом из них результат был равен
, то есть делился на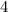 
.