20 көбейткіштерге жіктеңдер

(2a+b)²(a-2b)²

(p+
q)²-(p-q )²

( x+y)²-( y-z)²

( 4a-b)² ( 2a+3b )²

👇

Увидеть ответ

Ответ:

DiMOn4iK25

02.09.2021

Объяснение:

(2a+b)^2•(a-2b)^2=(4a^2+4ab+b^2)•(a^2-4ab+4b^2)=(4a^2+b^2)•(a^2+4b^2)=4a^4+4b^4

(p+q)^2-(p-q)^2=p^2+2pq+q^2-p^2-2pq+q^2=2q^2

(x+y)^2-(y-z)^2=x^2+2xy+y^2-y^2-2yz+z^2=x^2+x-z+y^2+z^2

(4a-b)^2•(2a+3b)^2=(16a^2-8ab+b^2)•(4a^2+12ab+9b^2)=64a^4-96ab+9b^4

4,5(41 оценок)

Открыть все ответы

Ответ:

MrStepWay

02.09.2021

Для решения запишем формулу бинома Ньютона:

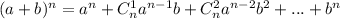
$(a+b)^n=a^n+C_n^1a^{n-1}b+C_n^2a^{n-2}b^2+...+b^n$

Если а - слагаемое, содержащее неизвестную в наибольшей степени, то для определения степени результата нужно рассмотреть выражение 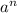a^n .

Если b - слагаемое, не содержащее неизвестную, то для определения свободного члена результата нужно рассмотреть выражение 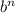b^n .

Рассмотрим многочлен $S(x)=P(x)\cdot Q(x)$ , где:

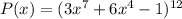
$P(x)=(3x^7+6x^4-1)^{12}$

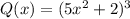
Q(x)=(5x^2+2)^3

Для определения степени и свободного члена произведения достаточно знать степень и свободный член каждого из множителей.

Для многочлена 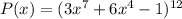$P(x)=(3x^7+6x^4-1)^{12}$ :

- степень определяется выражением 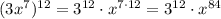$(3x^7)^{12}=3^{12}\cdot x^{7\cdot12}=3^{12}\cdot x^{84}$ , то есть степень равна 84

- свободный член равен $(-1)^{12}=1$

Для многочлена 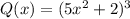Q(x)=(5x^2+2)^3 :

- степень определяется выражением 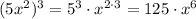$(5x^2)^3=5^3\cdot x^{2\cdot3}=125\cdot x^6$ , то есть степень равна 6

- свободный член равен 2^3=8

Наконец, для многочлена 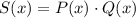$S(x)=P(x)\cdot Q(x)$ получим:

- степень определяется выражением 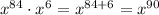$x^{84}\cdot x^6=x^{84+6}=x^{90}$ , то есть степень равна 90

- свободный член равен 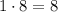$1\cdot8=8$

Сумма степени и свободного члена многочлена 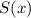S(x) :

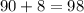
90+8=98

ответ: 98

4,5(17 оценок)

Ответ:

VicusiaKoval

02.09.2021

Задачи с решениями

1. Решить в целых числах уравнение x2 – xy – 2y2 = 7.

Решение

Запишем уравнение в виде (x – 2y)(x + y) = 7.

Так как х, у – целые числа, то находим решения исходного уравнения, как решения следующих четырёх систем:

1) x – 2y = 7, x + y = 1;

2) x – 2y = 1, x + y = 7;

3) x – 2y = –7, x + y = –1;

4) x – 2y = –1, x + y = –7.

Решив эти системы, получаем решения уравнения: (3; –2), (5; 2), (–3; 2) и (–5; –2).

ответ: (3; –2), (5; 2), (–3; 2), (–5; –2).

2. Решить в целых числах уравнение:

а) 20х + 12у = 2013;

б) 5х + 7у = 19;

в) 201х – 1999у = 12.

Решение

а) Поскольку при любых целых значениях х и у левая часть уравнения делится на два, а правая является нечётным числом, то уравнение не имеет решений в целых числах.

ответ: решений нет.

б) Подберём сначала некоторое конкретное решение. В данном случае, это просто, например,

x0 = 1, y0 = 2.

Тогда

5x0 + 7y0 = 19,

откуда

5(х – x0) + 7(у – y0) = 0,

5(х – x0) = –7(у – y0).

Поскольку числа 5 и 7 взаимно простые, то

х – x0 = 7k, у – y0 = –5k.

Значит, общее решение:

х = 1 + 7k, у = 2 – 5k,

где k – произвольное целое число.

ответ: (1+7k; 2–5k), где k – целое число.

в) Найти некоторое конкретное решение подбором в данном случае достаточно сложно. Воспользуемся алгоритмом Евклида для чисел 1999 и 201:

НОД(1999, 201) = НОД(201, 190) = НОД(190, 11) = НОД(11, 3) = НОД(3 , 2) = НОД(2, 1) = 1.

Запишем этот процесс в обратном порядке:

1 = 2 – 1 = 2 – (3 – 2) = 2·2 – 3 = 2· (11 – 3·3) – 3 = 2·11 – 7·3 = 2·11 – 7(190 – 11·17) =

= 121·11 – 7·190 = 121(201 – 190) – 7·190 = 121·201 – 128·190 =

= 121·201 – 128(1999 – 9·201) = 1273·201 – 128·1999.

Значит, пара (1273, 128) является решением уравнения 201х – 1999у = 1. Тогда пара чисел

x0 = 1273·12 = 15276, y0 = 128·12 = 1536

является решением уравнения 201х – 1999у = 12.

Общее решение этого уравнения запишется в виде

х = 15276 + 1999k, у = 1536 + 201k, где k – целое число,

или, после переобозначения (используем, что 15276 = 1283 + 7·1999, 1536 = 129 + 7·201),

х = 1283 + 1999n, у = 129 + 201n, где n – целое число.

ответ: (1283+1999n, 129+201n), где n – целое число.

3. Решить в целых числах уравнение:

а) x3 + y3 = 3333333;

б) x3 + y3 = 4(x2y + xy2 + 1).

Решение

а) Так как x3 и y3 при делении на 9 могут давать только остатки 0, 1 и 8 (смотрите таблицу в разделе «Делимость целых чисел и остатки»), то x3 + y3 может давать только остатки 0, 1, 2, 7 и 8. Но число 3333333 при делении на 9 даёт остаток 3. Поэтому исходное уравнение не имеет решений в целых числах.

ответ: целочисленных решений нет.

б) Перепишем исходное уравнение в виде (x + y)3 = 7(x2y + xy2) + 4. Так как кубы целых чисел при делении на 7 дают остатки 0, 1 и 6, но не 4, то уравнение не имеет решений в целых числах.

ответ: целочисленных решений нет.

4. Решить

а) в простых числах уравнение х2 – 7х – 144 = у2 – 25у;

б) в целых числах уравнение x + y = x2 – xy + y2.

Решение

а) Решим , получим, что x, y, z, u делятся на 2n при всех натуральных n, что возможно лишь при x = y = z = u = 0.

ответ: (0; 0; 0; 0).

7. Докажите, что уравнение

(х – у)3 + (y – z)3 + (z – x)3 = 30

не имеет решений в целых числах.

Решение

Воспользуемся следующим тождеством:

(х – у)3 + (y – z)3 + (z – x)3 = 3(х – у)(y – z)(z – x).

Тогда исходное уравнение можно записать в виде

(х – у)(y – z)(z – x) = 10.

Обозначим a = x – y, b = y – z, c = z – x и запишем полученное равенство в виде

abc = 10.

Кроме того очевидно, a + b + c = 0. Легко убедиться, что с точностью до перестановки из равенства abc = 10 следует, что числа |a|, |b|, |c| равны либо 1, 2, 5, либо 1, 1, 10. Но во всех этих случаях при любом выборе знаков a, b, c сумма a + b + c отлична от нуля. Таким образом, исходное уравнение не имеет решений в целых числах.

8. Решить в целых числах уравнение 1! + 2! + . . . + х! = у2.

Решение

Очевидно, что

если х = 1, то у2 = 1,

если х = 3, то у2 = 9.

Этим случаям соответствуют следующие пары чисел:

х1 = 1, у1 = 1;

х2 = 1, у2 = –1;

х3 = 3, у3 = 3;

х4 = 3, у4 = –3.

Заметим, что при х = 2 имеем 1! + 2! = 3, при х = 4 имеем 1! + 2! + 3! + 4! = 33 и ни 3, ни 33 не являются квадратами целых чисел. Если же х > 5, то, так как

5! + 6! + . . . + х! = 10n,

можем записать, что

1! + 2! + 3! + 4! + 5! + . . . + х! = 33 + 10n.

Так как 33 + 10n – число, оканчивающееся цифрой 3, то оно не является квадратом целого числа.

ответ: (1; 1), (1; –1), (3; 3), (3; –3).

9. Решите следующую систему уравнений в натуральных числах:

a3 – b3 – c3 = 3abc, a2 = 2(b + c).

Решение

Так как

3abc > 0, то a3 > b3 + c3;

таким образом имеем

b < a, c < a.