Её можно получить из графика гиперболы путём сдвига на 2 единицы влево вдоль оси ОХ.
Асимптота заданной гиперболы - прямая х= -2 .
Точки, через которые проходит график: (0,3) , (4,1) , (-4,-3) , (1,2) , (-1,6) , (-4,-3) .
На отрезке [0,4] наибольшее значение при х=0, а наименьшее - при х=4, так как на этом отрезке функция убывает и бОльшему значению аргумента (4>0) соответствует мЕньшее значение функции: y(4)<y(0).
B₁=3/q (3/q)*(1+q+q²)=10.5 3(1+q+q²)=10.5q 3+3q+3q²=10.5q 3q²-7.5q+3=0 q²-2.5q+1=0 D=(-2.5)²-4=6.25-4=2.25=1.5² q₁=(2.5-1.5)/2=1/2=0.5 не подходит, так как q=0.5 <1 q₂=(2.5+1.5)/2=4/2=2
Если дискриминант положительное, то квадратное уравнение имеет два действительных корня.Если дискриминант равен нулю, то квадратное уравнение имеет один единственный корень.Если дискриминант отрицательный, то квадратное уравнение действительных корня не имеет.
1) D > 0; 4p - 7 > 0 откуда p>7/4 - квадратное уравнение имеет два корня
2) D = 0; 4p - 7 =0 откуда p=7/4 - квадратное уравнение имеет один корень
3) D < 0 ⇒ p < 7/4 - квадратное уравнение не имеет корней.
Графиком функции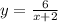 является гипербола.
является гипербола.
Её можно получить из графика гиперболы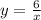 путём сдвига на 2 единицы влево вдоль оси ОХ.
путём сдвига на 2 единицы влево вдоль оси ОХ.
Асимптота заданной гиперболы - прямая х= -2 .
Точки, через которые проходит график: (0,3) , (4,1) , (-4,-3) , (1,2) , (-1,6) , (-4,-3) .
На отрезке [0,4] наибольшее значение при х=0, а наименьшее - при х=4, так как на этом отрезке функция убывает и бОльшему значению аргумента (4>0) соответствует мЕньшее значение функции: y(4)<y(0).
у(наибол)=у(0)=3 , у(наимен)=у(4)=1
На области определения функция убывающая.