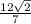Question

Найдите наибольшее и наименьшее значения функции f(x) = х^3- 2х^2 +х +3 на отрезке [0; 1,5].

Answer 1

$f(x)=x^3-2x^2+x+3\; \; \; ,\; \; \; x\in [\, 0\, ;\, 1,5\, ]\\\\f'(x)=3x^2-4x+1=0\; \; ,\; \; x_1=1\; ,\; \; x_2=\frac{1}{3}\\\\f(0)=3\\\\f(\frac{1}{3})=\frac{1}{27}-2\cdot \frac{1}{9}+\frac{1}{3}+3=\frac{85}{27}=3\frac{4}{27}\\\\f(1)=1-2+1+3=3\\\\f(1,5)=3,375-4,5+1,5+3=3,375=3\frac{3}{8}\\\\y(naibol)=y(1,5)=3,375\\\\y(naimen)=y(0)=y(1)=3$

Answer 2

Найдем  производную функции f'(x) = (х³-2х²+х+3)'=3х²-4х+1

3х²-4х+1=0

х₁,₂=(2±√(4-3))/3=(2±1)/3; х₁=1; х₂=1/3

1∈ [0;1,5]; 1/3∈ [0;1,5]

f(0) = 3 ;f(1/3) = (1/3)³- 2*(1/3)² +1/3 +3 =1/27-29+1/3+3=1/27-6/27+9/27+3=3 4/27

f(1) = 1- 2*1² +1+3 =3; f(3/2) = (3/2)³- 2*(3/2)² +3/2 +3 = 27/8-36/8+12/8+3=3 3/8

3 4/27=3 32/ (8*27);  3 3/8=3 81/(8*27);3 4/27< 3 3/8

Наибольшее значение функции на указанном отрезке равно f(1.5)= 3 3/8;

наименьшее f(1) =f(0) =3