ответ: (cos2x - sin^2x) / (2 * sin^2x - cos^2x) = - 1.
Объяснение:
1. Для того что бы упростить данное тригонометрическое выражение нам понадобится знание основных тригонометрических формул. В этом тригонометрическом выражении мы будем использовать вот эту формулу:
cos^2a + sin^2a = 1;
2. Подставим формулу cos^2a + sin^2a = 1, в тригонометрического выражения, получаем:
(cos2x - sin^2x) / (2 * sin^2x - cos^2x) = (cos^2a - sin^2a - sin^2a) / (2 * sin^2x - cos^2x) =
= ( - 2 * sin^2a + cos^2a) / (2 * sin^2x - cos^2x) =
= - (2 * sin^2x - cos^2x) / (2 * sin^2x - cos^2x) = - 1.
7; -4
Объяснение:
Решение методом подбора корней:
Записываем исходное уравнение:
(х - 7)(х + 4) = 0
Подбираем х:
х1 = 7, х2 = -4
Решение через раскрытие скобок, теорему Виета, и дискриминант:
Записываем исходное уравнение:
(х - 7)(х + 4) = 0
Раскрываем скобки:
х*х - 7x + 4x - 28 = 0
x^2 - 7x + 4x - 28 = 0
Приводим подобные:
x^2 - 3x - 28 = 0
1 под
Решаем через теорему Виета:
x1 + x2 = 3
x1*x2 = -28
Откуда:
x1 = 7, x2 = -4
2 под Решение через дискриминант
Записываем исходное уравнение:
x^2 - 3x - 28 = 0
Ищем дискриминант:
D = b^2 - 4ac
D = (-3)^2 -4*1*(-28)
D = 9 - (-112)
D = 9 + 112 = 121
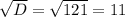
Находим корни уравнения:
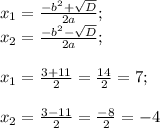
В данном решении показано решения данного уравнения. (причем имеет 2 под
ответ: 0.2125
Объяснение:
Раскрываем скобки по формуле сокращённого умножения:
Берём выражение 64c² - 2,25 для того, чтобы не запутаться при смене знаков. Далее раскрываем вторую скобку, перед которой стоит знак минус:
Находим подобные слагаемые и сокращаем их, получается: