Объяснение:
2.1.
3x^2 +bx+12=0
D=b^2 -144
Уравнение не будет иметь корней при D<0.
b^2 -144<0
(b-12)(b+12)<0
b-12<0
b1<12
Проверка:
b^2 -144=0^2 -144=0-144=-144; -144<0
b+12<0
b2<-12
Проверка:
b^2 -144=(-20)^2 -144=400-144=256; 256>0
Вывод: уравнение не имеет решений при -12<b<12.
ответ: b принадлежит (-12; 12).
2.2.
x - оценка за последующую работу.
(7+8+7+9+6+x)/6=8
37+x=8•6
x=48-37=11
2.3.
Используем формулы арифметической прогрессии.
Система уравнений:
a5=a1+(5-1)d; -0,8=a1+4d
a11=a1+(11-1)d; -5=a1+10d
-5-(-0,8)=a1+10d-a1-4d
6d=-4,2
d=-4,2÷6=-0,7
-5=a1+10•(-0,7)
-5=a1-7
a1=-5+7=2
Сумма 20-х членов арифметической прогрессии:
S20=(2a1+d(20-1))/2 •20=(2•2+(-0,7)•19)/2 •20=(4-13,3)/2 •20=--9,3/2 •20=-4,65•20=-93
Из 9 солдат нужно выбрать некоторых 7. Число сделать это равно числу сочетаний из 9 элементов по 7:
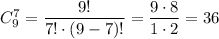
Из 6 сержантов нужно выбрать некоторых 4. Число сделать это равно числу сочетаний из 6 элементов по 4:
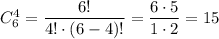
Из 4 офицеров нужно выбрать некоторого 1. Число сделать это равно числу сочетаний из 4 элементов по 1:
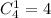
Так как выбор солдат, выбор сержантов и выбор офицера попарно независимы, то соответствующие нужны перемножить. То есть любому выбору солдат мы можем сопоставить любой выбор сержантов, а также любой выбор офицера.
Общее число вариантов:
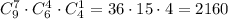
ответ: 2160 вариантов
В решении.
Объяснение:
а) Преобразуйте выражение, чтобы получить многочлен стандартного вида. Укажите степень многочлена.
(2х² - 2)² - 4х³(х³ + х² - х - 2) + 4(х²)³ + 20х⁹/5х⁴ - 2(4х³ + 1) =
= 4х⁴ - 8х² + 4 - 4х⁶ - 4х⁵ + 4х⁴ + 8х³ + 4х⁶ + 4х⁵ - 8х³ - 2 =
= 8х⁴ - 8х² + 2. Стандартный вид. Степень (х⁴) = 4.
б) Докажите, что при любых целых значениях x многочлен делится на 2.
Так как коэффициенты при х чётные (8 и 8) и число 2 также чётное, при любых значениях х многочлен делится на 2.
в) Докажите, что при любых действительных значениях x многочлен не может принимать отрицательных значений.
Так как 8х⁴ > 8х² и степени при х чётные, то есть, сами одночлены в составе многочлена не могут быть отрицательными, при любых действительных значениях x многочлен не может принимать отрицательных значений.
Решение во вложении. Две фотки.