x=1
Объяснение:
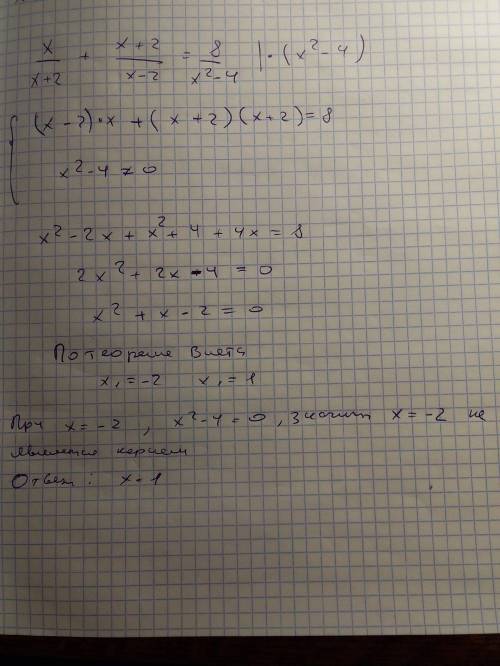
у = kx+b
A(5; 3)
B(-3; -1)
Подставим координаты точек А и В в уравнение прямой вместо х и у, но точек две, поэтому уравнений получим тоже два с двумя неизвестными k и b
Составим систему уравнений и решим её:
{5k+b=3
{-3k+b=-1
вычтем из верхнего уравнения нижнее, получим
8k+0=4
k = 2
подставим k=2 в любое уравнение системы, например, в верхнее, получим:
5*2 + b =3
10+b = 3
b = 7
Запишем уравнение прямой:
у = 2х+7, которая проходит через данные точки А и В.
Далее, просили уравнение прямой, которая
1) параллельная данной, а значит её коэффициент k одинаковые, т е k = 2 и
2) пересекает ось абсцисс в точке (-10; 0)
0 = 2*(-10) + b
0 = -20 + b
b = 20
y = kx+b
k= 2, b= 20
y = 2x+20 - искомая формула прямой
1. -2;
2. 3.
Объяснение:
1.Sn=6n-n^2
a1 = S1 = 6•1 - 1^2 = 5;
a1+a2 = S2 = 6•2 - 2^2 = 12 - 4 = 8;
a2 = S2 - S1 = 8 - 5 = 3.
Найдём d:
d = a2 - a3 = 3 - 5 = -2.
2. Sn=6n-n^2
Рассмотрим квадратичную функцию
у = 6х - х^2.
Графиком функции является парабола
у = - х^2 + 6х
Ветви параболы направлены вниз, своего наибольшего значения функция достигает в вершине параболы. Найдём её координаты:
х вершины = -b/(2a) = -6/(-2) = 3.
y вершины = - 3^2 +6•3 = -9+18 = 9.
Наибольшего значения 9 функция у = - х^2 + 6х достигает при х = 3.
Так как 3 - натуральное число, то и наша функция Sn=6n-n^2, определённая только для натуральных n, достигает наибольшего значения 9 при n = 3.
Необходимо взять три первых члена прогрессии, чтобы их сумма была наибольшей и равной 9.
ответить на второй вопрос можно и по-прежнему другому:
Sn=6n-n^2
- n^2 + 6n = - (n^2 - 6n) = - (n^2 -2•n•3 + 9 - 9) = - ((n-3)^2 -9) = - (n-3)^2 + 9.
Так как слагаемое 9 постоянно, a - (n-3)^2 неположительно для любого n, то наибольшей сумма будет тогда, когда наибольшим будет первое слагаемое, т.е. когда - (n-3)^2 = 0, при n = 3.
В этом случае Sn = - (n-3)^2 + 9 = 0 + 9 = 9.
ОДЗ: x≠±2
x(x-2)+(x+2)²=8
x²-2x+x²+4x+4-8=0
2x²+2x-4=0
x²+x-2=0
D= 1+8= 9
x1= (-1+3)/2= 1
x2= (-1-3)/2= -2 - не корень