1) 7 легковых, 15 грузовых машин
Объяснение:
Задача 1.
Мы знаем что общее количество отремонтированных машин составляет 22.
Возьмём количество грузовых машин как х. А количество легковых как (х-8). С этих данных составим уравнение:
х + х-8 = 22,
2х-8=22,
2х=22+8,
2х=30,
х=30:2,
х=15.
15 - это количество грузовых машин.
теперь 15 - 8 = 7 машин - это легковые машины.
Задача 2.
Нам известно, что общее количество выпущенных изделий равно 1315. Изделия в январе обозначим через х. А изделия в феврале обозначим через (х+165). По этим данным составим уравнение:
х + х+165 = 1315,
2х+165=1315,
2х=1315-165,
2х=1150,
х=1150:2,
х=575.
575 - это количество изделий выпущенных в январе.
тогда 575+165= 740. это количество изделий выпущенных в феврале.
В январе - 572
В феврале - 740.
1) 7 легковых, 15 грузовых машин
Объяснение:
Задача 1.
Мы знаем что общее количество отремонтированных машин составляет 22.
Возьмём количество грузовых машин как х. А количество легковых как (х-8). С этих данных составим уравнение:
х + х-8 = 22,
2х-8=22,
2х=22+8,
2х=30,
х=30:2,
х=15.
15 - это количество грузовых машин.
теперь 15 - 8 = 7 машин - это легковые машины.
Задача 2.
Нам известно, что общее количество выпущенных изделий равно 1315. Изделия в январе обозначим через х. А изделия в феврале обозначим через (х+165). По этим данным составим уравнение:
х + х+165 = 1315,
2х+165=1315,
2х=1315-165,
2х=1150,
х=1150:2,
х=575.
575 - это количество изделий выпущенных в январе.
тогда 575+165= 740. это количество изделий выпущенных в феврале.
В январе - 572
В феврале - 740.
4 см - ширина
9 см - длина
Объяснение:
Пусть x (см) - ширина, тогда (x + 5) - длина. Так как площадь прямоугольника находится по формуле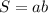 (где a - длина, b - ширина), то составим и решим уравнение:
(где a - длина, b - ширина), то составим и решим уравнение: